题目内容
18.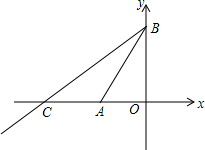 如图,在平面直角坐标系中,点A(-1,0),B(0,3),直线BC交坐标轴于B,C,且∠CBA=45°,求直线BC的解析式.
如图,在平面直角坐标系中,点A(-1,0),B(0,3),直线BC交坐标轴于B,C,且∠CBA=45°,求直线BC的解析式.
分析 作AD⊥BC于D,由A、B的坐标可知OA=1,OB=3,根据勾股定理AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{10}$,BD=AD=$\sqrt{\frac{1}{2}A{B}^{2}}$=$\sqrt{5}$,设AC=x,则OC=x+1,DC=$\sqrt{{x}^{2}-5}$,BC=$\sqrt{{x}^{2}-5}$+$\sqrt{5}$,在RT△OBC中,根据勾股定理得出OC2+OB2=BC2,即(x+1)2+32=($\sqrt{{x}^{2}-5}$+$\sqrt{5}$),解得x1=-$\frac{5}{2}$(舍去),x2=5,求得OC=6,得出C(-6,0),然后根据待定系数法即可求得BC的解析式.
解答 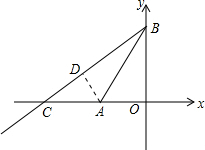 解:作AD⊥BC于D,
解:作AD⊥BC于D,
∵点A(-1,0),B(0,3),
∴OA=1,OB=3,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{10}$,
∵∠CBA=45°,
∴△ABD是等腰直角三角形,
∴BD=AD=$\sqrt{\frac{1}{2}A{B}^{2}}$=$\sqrt{5}$,
设AC=x,则OC=x+1,
∴DC=$\sqrt{{x}^{2}-5}$,
∴BC=$\sqrt{{x}^{2}-5}$+$\sqrt{5}$,
在RT△OBC中,OC2+OB2=BC2,即(x+1)2+32=($\sqrt{{x}^{2}-5}$+$\sqrt{5}$),
解得x1=-$\frac{5}{2}$(舍去),x2=5,
∴AC=5,OC=6,
∴C(-6,0),
设直线BC的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{-6k+b=0}\\{b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=3}\end{array}\right.$,
∴直线BC的解析式为y=$\frac{1}{2}$x+3.
点评 本题考查了待定系数法求一次函数的解析式以及勾股定理的应用,作出辅助线构建等腰直角三角形是解题的关键.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案| 车速v(km/h) | 40 | 50 |
| 刹车距离s乙(m) | 12 | 17.5 |
(2)若乙车在限速120km/h的高速公路上行驶,乙车的最长刹车距离是多少m?
(3)刹车速度是处理交通事故的一个重要因素,请看下面一个交通事故案例:甲、乙两车在限速为80km/g的道路上相向而行,等望见对方,同时刹车时已晚,两车还是相撞了,事后经现场勘查,测得甲车的刹车距离超过16m,但小于18m,乙车的刹车距离是24m,请你比较两车的速度,并判断哪辆车超速?
| 工厂 | A地 | B地 | C地 |
| 运费 | 30元/件 | 8元/件 | 25元/件 |
①根据信息填表:
| A地 | B地 | C地 | 合计 | |
| 产品件数(件) | x | 200-3x | 2x | 200 |
| 运费(元) | 30x | -24x+1600 | 50x | 56x+1600 |
(2)若总运费为5800元,求n的最小值.
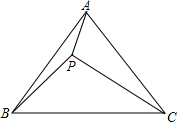 如图所示,设点P为△ABC内一点,∠PBA=10°,∠PCB=30°,∠BAP=20°,∠CBP=40°,求证:△ABC是等腰三角形.
如图所示,设点P为△ABC内一点,∠PBA=10°,∠PCB=30°,∠BAP=20°,∠CBP=40°,求证:△ABC是等腰三角形.