题目内容
15.若方程组$\left\{\begin{array}{l}{3m+n=k}\\{m+3n=2}\end{array}\right.$的解m,n满足m+n<2,求k的取值范围.分析 解方程组求出m+n的值,再根据m+n<2,得到不等式,即可解答.
解答 解:$\left\{\begin{array}{l}{3m+n=k①}\\{m+3n=2②}\end{array}\right.$,
①+②得:m+n=$\frac{k+2}{4}$
∵m+n<2,
∴$\frac{k+2}{4}$<2,
解得:k<6.
点评 本题考查了二元一次方程组的解,解决本题的关键是求出二元一次方程组的解.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
5.某工厂欲将n件产品运往A、B、C三地销售,要求运往C地的件数是运往A地的件数的2倍,各地的运费如表所示.设安排x件产品运往A地.
(1)当n=200时:
①根据信息填表:
②若运往B地的件数不多于运往C地的件数,总运费不超过4000元,则有哪几种运输方案?
(2)若总运费为5800元,求n的最小值.
| 工厂 | A地 | B地 | C地 |
| 运费 | 30元/件 | 8元/件 | 25元/件 |
①根据信息填表:
| A地 | B地 | C地 | 合计 | |
| 产品件数(件) | x | 200-3x | 2x | 200 |
| 运费(元) | 30x | -24x+1600 | 50x | 56x+1600 |
(2)若总运费为5800元,求n的最小值.
6. 如图,在△ABC中,AB=AC,EF∥BC,∠A=40°,则∠AEF的度数是( )
如图,在△ABC中,AB=AC,EF∥BC,∠A=40°,则∠AEF的度数是( )
 如图,在△ABC中,AB=AC,EF∥BC,∠A=40°,则∠AEF的度数是( )
如图,在△ABC中,AB=AC,EF∥BC,∠A=40°,则∠AEF的度数是( )| A. | 40° | B. | 50° | C. | 70° | D. | 140° |
20.一辆汽车在直路上行驶,两次拐弯后,仍按原来的方向行驶,那么这两次拐弯是( )
| A. | 第一次向右拐30°,第二次向右拐30° | |
| B. | 第一次向右拐30°,第二次向右拐150° | |
| C. | 第一次向左拐30°,第二次向右拐150° | |
| D. | 第一次向左拐30°,第二次向右拐30° |
7.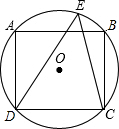 如图,⊙O是正方ABCD的外接圆,点E是弧AB上任意一点,则∠DEC的度数为( )
如图,⊙O是正方ABCD的外接圆,点E是弧AB上任意一点,则∠DEC的度数为( )
 如图,⊙O是正方ABCD的外接圆,点E是弧AB上任意一点,则∠DEC的度数为( )
如图,⊙O是正方ABCD的外接圆,点E是弧AB上任意一点,则∠DEC的度数为( )| A. | 40° | B. | 45° | C. | 48° | D. | 50° |
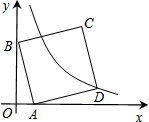 如图,在平面直角坐标系中,A(1,0),B(0,3),以AB为边在第一象限作正方形ABCD,点D在双曲线y=$\frac{k}{x}$(k≠0)上,将正方形沿x轴负方向平移m个单位长度后,点C恰好落在双曲线上,则m的值是2.
如图,在平面直角坐标系中,A(1,0),B(0,3),以AB为边在第一象限作正方形ABCD,点D在双曲线y=$\frac{k}{x}$(k≠0)上,将正方形沿x轴负方向平移m个单位长度后,点C恰好落在双曲线上,则m的值是2.