题目内容
1.解不等式组:$\left\{\begin{array}{l}{\frac{2}{3}x+5>1-x}\\{x-1≤\frac{3}{4}x-\frac{1}{8}}\end{array}\right.$.分析 首先解每个不等式,两个不等式的解集的公共部分就是所求不等式组的解集.
解答 解:$\left\{\begin{array}{l}{\frac{2}{3}x+5>1-x…①}\\{x-1≤\frac{3}{4}x-\frac{1}{8}…②}\end{array}\right.$,
解①得:x>3,
解②得:x≤$\frac{7}{2}$.
则不等式组的解集是:3<x≤$\frac{7}{2}$.
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
相关题目
11.在实数$\sqrt{3}$,$\root{3}{-8}$,$\frac{22}{7}$,$\frac{π}{3}$,0.2020020002….(每两个相邻的2中间依次多一个0)中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.某工厂欲将n件产品运往A、B、C三地销售,要求运往C地的件数是运往A地的件数的2倍,各地的运费如表所示.设安排x件产品运往A地.
(1)当n=200时:
①根据信息填表:
②若运往B地的件数不多于运往C地的件数,总运费不超过4000元,则有哪几种运输方案?
(2)若总运费为5800元,求n的最小值.
| 工厂 | A地 | B地 | C地 |
| 运费 | 30元/件 | 8元/件 | 25元/件 |
①根据信息填表:
| A地 | B地 | C地 | 合计 | |
| 产品件数(件) | x | 200-3x | 2x | 200 |
| 运费(元) | 30x | -24x+1600 | 50x | 56x+1600 |
(2)若总运费为5800元,求n的最小值.
6. 如图,在△ABC中,AB=AC,EF∥BC,∠A=40°,则∠AEF的度数是( )
如图,在△ABC中,AB=AC,EF∥BC,∠A=40°,则∠AEF的度数是( )
 如图,在△ABC中,AB=AC,EF∥BC,∠A=40°,则∠AEF的度数是( )
如图,在△ABC中,AB=AC,EF∥BC,∠A=40°,则∠AEF的度数是( )| A. | 40° | B. | 50° | C. | 70° | D. | 140° |
 已知,如图,?ABCD中,CN=AM,AE=CF,求证:EN∥MF.
已知,如图,?ABCD中,CN=AM,AE=CF,求证:EN∥MF.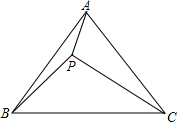 如图所示,设点P为△ABC内一点,∠PBA=10°,∠PCB=30°,∠BAP=20°,∠CBP=40°,求证:△ABC是等腰三角形.
如图所示,设点P为△ABC内一点,∠PBA=10°,∠PCB=30°,∠BAP=20°,∠CBP=40°,求证:△ABC是等腰三角形.