题目内容
15.对于函数y=$\frac{4}{x}$,当x=$\frac{1}{2}$时,y=8.分析 直接把x=$\frac{1}{2}$代入函数y=$\frac{4}{x}$求出y的值即可.
解答 解:当x=$\frac{1}{2}$时,y=$\frac{4}{\frac{1}{2}}$=8.
故答案为:8.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
14.若方程(2a+1)x2+bx+c=0是关于x的一元一次方程,则字母系数a,b,c的值必须满足( )
| A. | a=-$\frac{1}{2}$,b≠0,c为任何数 | B. | a≠$\frac{1}{2}$,b≠0,c=0 | ||
| C. | a=-$\frac{1}{2}$,b≠0,c≠0 | D. | a=$\frac{1}{2}$,b=0,c为任何数 |
3.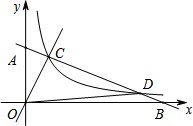 如图,在平面直角坐标系中,直线AB与双曲线$y=\frac{2}{x}$相交于C、D两点,已知直线OC解析式为y=2x,S△AOD=6,则D点的坐标为( )
如图,在平面直角坐标系中,直线AB与双曲线$y=\frac{2}{x}$相交于C、D两点,已知直线OC解析式为y=2x,S△AOD=6,则D点的坐标为( )
 如图,在平面直角坐标系中,直线AB与双曲线$y=\frac{2}{x}$相交于C、D两点,已知直线OC解析式为y=2x,S△AOD=6,则D点的坐标为( )
如图,在平面直角坐标系中,直线AB与双曲线$y=\frac{2}{x}$相交于C、D两点,已知直线OC解析式为y=2x,S△AOD=6,则D点的坐标为( )| A. | $(3,\frac{2}{3})$ | B. | $(4,\frac{1}{2})$ | C. | $(5,\frac{2}{5})$ | D. | $(6,\frac{1}{3})$ |
10.已知反比例函数y=-$\frac{1}{x}$,下列结论正确的是( )
| A. | y的值随着x的增大而减小 | |
| B. | 图象是双曲线,是中心对称图形且是轴对称 | |
| C. | 当x>1时,0<y<1 | |
| D. | 图象可能与坐标轴相交 |
7.一个钝角三角形的两边长为5、12,则第三边可以为( )
| A. | 11 | B. | 13 | C. | 15 | D. | 17 |
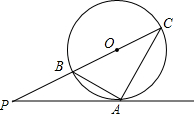 如图,P为⊙0外一点,A为⊙0上一点,直线OP交⊙0于B、C,连接AB、AC,且∠PAB=∠C.
如图,P为⊙0外一点,A为⊙0上一点,直线OP交⊙0于B、C,连接AB、AC,且∠PAB=∠C.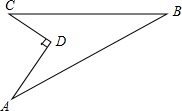 如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?
如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?