题目内容
20.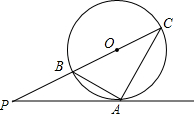 如图,P为⊙0外一点,A为⊙0上一点,直线OP交⊙0于B、C,连接AB、AC,且∠PAB=∠C.
如图,P为⊙0外一点,A为⊙0上一点,直线OP交⊙0于B、C,连接AB、AC,且∠PAB=∠C.(1)说明:直线PA与⊙0相切.
(2)若PA=2,PB=1时,求⊙0的半径.
分析 (1)连接OA,根据直径所对的圆周角等于90°,可得出∠OAB+∠OAC=90°,根据等边对等角得出∠OAC=∠OCA,再由∠PAB=∠C得出∠PAO=90°,即可得出直线PA与⊙0相切;
(2)设⊙0的半径为r,在Rt△PAO中,利用勾股定理可得出关于r的方程,解方程即可得出⊙0的半径.
解答 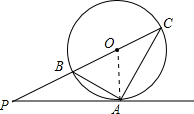 解:(1)证明:连接OA,
解:(1)证明:连接OA,
∵BC为⊙O的直径,
∴∠BAC=90°,
即∠OAB+∠OAC=90°,
∵OA=OC,
∴∠OAC=∠OCA,
∵∠PAB=∠C,
∴∠OAB+∠PAB=90°,
即∠PAO=90°,
∴直线PA与⊙0相切;
(2)设⊙0的半径为r,
∵直线PA与⊙0相切
∴∠PAO=90°,
在Rt△PAO中,OA2+PA2=OP2,
∵PA=2,PB=1,
∴r2+22=(r+1)2,
解得r=$\frac{3}{2}$,
∴⊙0的半径$\frac{3}{2}$.
点评 本题考查了切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
10.下列方程是一元一次方程的是( )
| A. | 2x-y=$\frac{1}{2}$ | B. | x2-x=1 | C. | x+$\frac{1}{2x}$=3 | D. | x=1 |
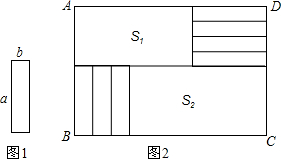 将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1,S2,已知小长方形纸片的长为a,宽为b,且a>b.
将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1,S2,已知小长方形纸片的长为a,宽为b,且a>b.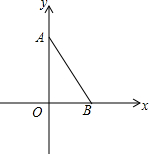 如图,在平面直角坐标系中,已知A(0,4),B(2,0),在第一象限内的点C,使△ABC为面积最小的等腰直角三角形,则点C的坐标为(3,3),最小面积为5.
如图,在平面直角坐标系中,已知A(0,4),B(2,0),在第一象限内的点C,使△ABC为面积最小的等腰直角三角形,则点C的坐标为(3,3),最小面积为5.