题目内容
7.一个钝角三角形的两边长为5、12,则第三边可以为( )| A. | 11 | B. | 13 | C. | 15 | D. | 17 |
分析 设第三边为c,根据三角形的三边关系求出c的取值范围,再由三角形是钝角可求得c的最小值即可解题.
解答 解:设第三边为c,
若这个三角形为直角三角形,则第三边=$\sqrt{{5}^{2}+{12}^{2}}$=13.
∵钝角大于直角,
∴c>13,
∵三角形第三边小于其余两边和,
∴c<17,
∴第三边可以为15.
故选C.
点评 本题考查的是勾股定理,考查了三角形三边关系,本题中根据勾股定理求c>13是解题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
2.下列说法中不正确的个数有( )
①1是绝对值最小的有理数;
②若a2=b2,则a3=b3;
③两个四次多项式的和一定是四次多项式;
④多项式x2-3kxy-3y2+$\frac{1}{3}$xy-8合并同类项后不含xy项,则k的值是$\frac{1}{9}$.
①1是绝对值最小的有理数;
②若a2=b2,则a3=b3;
③两个四次多项式的和一定是四次多项式;
④多项式x2-3kxy-3y2+$\frac{1}{3}$xy-8合并同类项后不含xy项,则k的值是$\frac{1}{9}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.若多项式3x2-7x2+6x-5x+3与多项式ax2-3ax2+2bx+x+c相等(其中a,b,c是常数),则a,b,c的值为( )
| A. | a=2,b=0,c=3 | B. | a=-2,b=0,c=3 | C. | a=2,b=-1,c=3 | D. | a=2,b=0,c=4 |
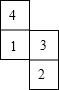 如图,这是一个由小正方块搭成的几何体的从上面看到的形状图,小正方形中的数字表示在该位置小立方体的个数,请你分别画出从正面、左面看到的形状图.
如图,这是一个由小正方块搭成的几何体的从上面看到的形状图,小正方形中的数字表示在该位置小立方体的个数,请你分别画出从正面、左面看到的形状图.