题目内容
5.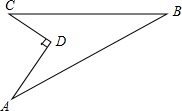 如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?
如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?
分析 连接AC,根据勾股定理求出AC,根据勾股定理的逆定理求出∠ACB=90°,求出区域的面积,即可求出答案.
解答 解:连结AC, 如图所示:
如图所示:
在Rt△ACD中,∠ADC=90°,AD=4米,CD=3米,
由勾股定理得:AC=$\sqrt{{8}^{2}+{6}^{2}}$=10(米),
∵AC2+BC2=102+242=676,AB2=262=676,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴该区域面积S=S△ACB-S△ADC=$\frac{1}{2}$×10×24-$\frac{1}{2}$×6×8=96(平方米),
∴铺满这块空地共需花费=96×100=9600元.
点评 本题考查了勾股定理,三角形面积,勾股定理的逆定理的应用;解此题的关键是求出区域的面积.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
13.若-3xmy2n与2xy6是同类项,则m-n的值为( )
| A. | -2 | B. | 2 | C. | -4 | D. | 4 |
10.下列方程是一元一次方程的是( )
| A. | 2x-y=$\frac{1}{2}$ | B. | x2-x=1 | C. | x+$\frac{1}{2x}$=3 | D. | x=1 |
17.若多项式3x2-7x2+6x-5x+3与多项式ax2-3ax2+2bx+x+c相等(其中a,b,c是常数),则a,b,c的值为( )
| A. | a=2,b=0,c=3 | B. | a=-2,b=0,c=3 | C. | a=2,b=-1,c=3 | D. | a=2,b=0,c=4 |
14. 如图,在△ABC中,DE垂直平分AC,若BC=20cm,AB=12cm,则△ABD的周长为( )
如图,在△ABC中,DE垂直平分AC,若BC=20cm,AB=12cm,则△ABD的周长为( )
 如图,在△ABC中,DE垂直平分AC,若BC=20cm,AB=12cm,则△ABD的周长为( )
如图,在△ABC中,DE垂直平分AC,若BC=20cm,AB=12cm,则△ABD的周长为( )| A. | 20cm | B. | 22cm | C. | 26cm | D. | 32cm |
 已知四边形ABCD,E,F分别是BD,AC的中点,若四边形ABCD的面积是2016,则四边形AEFD的面积为多少?
已知四边形ABCD,E,F分别是BD,AC的中点,若四边形ABCD的面积是2016,则四边形AEFD的面积为多少?