题目内容
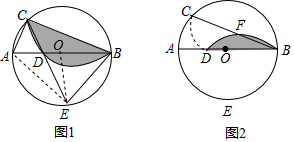
15. 如图,点A的坐标为(1,2),AB⊥x轴于点B,将△AOB绕点A逆时针旋转90°得到△ACD,双曲线y=$\frac{k}{x}$(x>0)恰好经过点C,交AD于点E,则点E的坐标为($\frac{3}{2}$,2).
如图,点A的坐标为(1,2),AB⊥x轴于点B,将△AOB绕点A逆时针旋转90°得到△ACD,双曲线y=$\frac{k}{x}$(x>0)恰好经过点C,交AD于点E,则点E的坐标为($\frac{3}{2}$,2).
分析 根据点A的坐标求出OB、AB,根据旋转的性质可得AD=AB,CD=OB,然后求出点C的横坐标与纵坐标,从而得到点C的坐标,利用待定系数法求出反比例函数解析式,再根据点E的纵坐标利用反比例函数解析式求出横坐标,从而得解.
解答 解:∵点A的坐标为(1,2),AB⊥x轴于点B,
∴OB=1,AB=2,
∵△AOB绕点A逆时针旋转90°得到△ACD,
∴AD=AB=2,CD=OB=1,
∴点C的横坐标为1+2=3,
纵坐标为2-1=1,
∴点C的坐标为(3,1),
∵双曲线y=$\frac{k}{x}$(x>0)恰好经过点C,
∴$\frac{k}{3}$=1,
解得k=3,
所以,双曲线为y=$\frac{3}{x}$,
∵△AOB绕点A逆时针旋转90°得到△ACD,双曲线y=$\frac{k}{x}$(x>0)交AD于点E,
∴点E的纵坐标为2,
∴$\frac{3}{x}$=2,
解得x=$\frac{3}{2}$,
∴点E的坐标为($\frac{3}{2}$,2).
故答案为:($\frac{3}{2}$,2).
点评 本题考查了坐标与图形变化-旋转,反比例函数图象上点的坐标特征,熟记旋转的性质并求出点C的坐标是解题的关键,也是本题的难点.

练习册系列答案
相关题目
5.某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入,下表是某周的实际生产量与计划量的差值:
(1)根据记录的数据可知该厂星期四生产自行车多少辆?
(2)根据记录的数据可知该厂本周实际生产自行车多少辆?
(3)产量最多的一天比产量最少的一天多生产多少辆自行车?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 生产量与计划量的差值 | +5 | -2 | -4 | +13 | -10 | +14 | -9 |
(2)根据记录的数据可知该厂本周实际生产自行车多少辆?
(3)产量最多的一天比产量最少的一天多生产多少辆自行车?
10.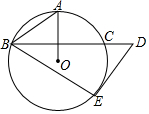 如图,OA是⊙O的半径,BC是⊙O的弦,且BC⊥OA,过BC的延长线上一点D作⊙O的切线DE,切点为E,连接AB,BE,若∠BDE=52°,则∠ABE的度数是( )
如图,OA是⊙O的半径,BC是⊙O的弦,且BC⊥OA,过BC的延长线上一点D作⊙O的切线DE,切点为E,连接AB,BE,若∠BDE=52°,则∠ABE的度数是( )
 如图,OA是⊙O的半径,BC是⊙O的弦,且BC⊥OA,过BC的延长线上一点D作⊙O的切线DE,切点为E,连接AB,BE,若∠BDE=52°,则∠ABE的度数是( )
如图,OA是⊙O的半径,BC是⊙O的弦,且BC⊥OA,过BC的延长线上一点D作⊙O的切线DE,切点为E,连接AB,BE,若∠BDE=52°,则∠ABE的度数是( )| A. | 52° | B. | 58° | C. | 60° | D. | 64° |
20.计算|-6|-(-$\frac{1}{3}$)0的值是( )
| A. | 5 | B. | -5 | C. | 5$\frac{2}{3}$ | D. | 7 |
7.若关于x的一元二次方程$\frac{\sqrt{3}}{4}$x2+$\sqrt{3}$x+tana=0有两个相等的实数根,则锐角a等于( )
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
5.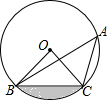 如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
 如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )| A. | π-2 | B. | $\frac{2}{3}π-1$ | C. | π-4 | D. | $\frac{2}{3}π-2$ |
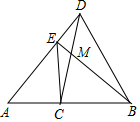 如图,已知点C为线段AB的中点,以BC为边作△DBC,使DC=DB,连接AD,过点C作CE⊥AB交AD于点E,连接BE交CD于点M.
如图,已知点C为线段AB的中点,以BC为边作△DBC,使DC=DB,连接AD,过点C作CE⊥AB交AD于点E,连接BE交CD于点M.