题目内容
2.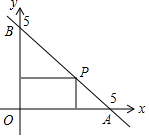 如图,一次函数的图象与两坐标轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长是( )
如图,一次函数的图象与两坐标轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长是( )| A. | 5 | B. | 7.5 | C. | 10 | D. | 25 |
分析 根据待定系数法求得直线AB的解析式y=-x+5,设P点坐标为(m,-m+5),然后根据周长公式可得出答案.
解答  解:∵A(5,0),B(0,5),
解:∵A(5,0),B(0,5),
∴直线AB的解析式为y=-x+5,
∵P是线段AB上任意一点(不包括端点),
∴设P点坐标为(m,-m+5),
如图,过P点分别作PD⊥x轴,PC⊥y轴,垂足分别为D、C,
∵P点在第一象限,
∴PD=-m+5,PC=m,
∴矩形PDOC的周长为:2(m-m+5)=10,
故选C.
点评 本题主要考查矩形的性质及一次函数图象上点的坐标特征,根据待定系数法求得直线AB的关系是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
10.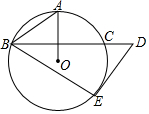 如图,OA是⊙O的半径,BC是⊙O的弦,且BC⊥OA,过BC的延长线上一点D作⊙O的切线DE,切点为E,连接AB,BE,若∠BDE=52°,则∠ABE的度数是( )
如图,OA是⊙O的半径,BC是⊙O的弦,且BC⊥OA,过BC的延长线上一点D作⊙O的切线DE,切点为E,连接AB,BE,若∠BDE=52°,则∠ABE的度数是( )
 如图,OA是⊙O的半径,BC是⊙O的弦,且BC⊥OA,过BC的延长线上一点D作⊙O的切线DE,切点为E,连接AB,BE,若∠BDE=52°,则∠ABE的度数是( )
如图,OA是⊙O的半径,BC是⊙O的弦,且BC⊥OA,过BC的延长线上一点D作⊙O的切线DE,切点为E,连接AB,BE,若∠BDE=52°,则∠ABE的度数是( )| A. | 52° | B. | 58° | C. | 60° | D. | 64° |
7.若关于x的一元二次方程$\frac{\sqrt{3}}{4}$x2+$\sqrt{3}$x+tana=0有两个相等的实数根,则锐角a等于( )
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
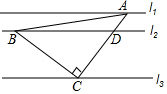 已知直线l1∥l2∥l3,等腰直角△ABC的三个顶点A,B,C分别在l1,l2,l3上,若∠ACB=90°,l1,l2的距离为1,l2,l3的距离为3,
已知直线l1∥l2∥l3,等腰直角△ABC的三个顶点A,B,C分别在l1,l2,l3上,若∠ACB=90°,l1,l2的距离为1,l2,l3的距离为3,