题目内容

5．若（x-a）（x-b）=x2+mx+n，则m，n的值分别是（　　）
A．m=a+b，n=abB．m=a+b，n=-abC．m=-（a+b），n=abD．m=-（a+b），n=-ab

分析 根据多项式与多项式相乘的法则进行计算，对应相等即可得到答案．

解答 解：（x-a）（x-b）=x2-（a+b）x+ab，
∴m=-（a+b），n=ab，
故选：C．

点评 本题考查的是多项式乘多项式，多项式与多项式相乘的法则：多项式与多项式相乘，先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加．

练习册系列答案
相关题目
20．有这样一个问题：如图，在四边形ABCD中，AB=AD，CB=CD，我们把这种两组邻边分别相等的四边形叫做筝形．请探究筝形的性质与判定方法．
小南根据学习四边形的经验，对筝形的性质和判定方法进行了探究．
下面是小南的探究过程：
（1）由筝形的定义可知，筝形的边的性质是：筝形的两组邻边分别相等，关于筝形的角的性质，通过测量，折纸的方法，猜想：筝形有一组对角相等，请将下面证明此猜想的过程补充完整；
已知：如图，在筝形ABCD中，AB=AD，CB=CD．
求证：∠B=∠D．
证明：连接AC，
在△ABC和△ADC中，
$\left\{\begin{array}{l}\;AB=AD\\ \;BC=DC\\ AC=AC\end{array}\right.$，
∴△ABC≌△ADC（SSS），
∴∠B=∠D
由以上证明可得，筝形的角的性质是：筝形有一组对角相等．
（2）连接筝形的两条对角线，探究发现筝形的另一条性质：筝形的一条对角线平分另一条对角线．结合图形，写出筝形的其他性质（一条即可）：筝形的两条对角线互相垂直．
（3）筝形的定义是判定一个四边形为筝形的方法之一．从边、角、对角线或性质的逆命题等角度可以进一步探究筝形的判定方法，请你写出筝形的一个判定方法（定义除外），并说明你的结论．
1．已知在四边形ABCD中，点E、F分别是BC、CD边上的一点．
（1）如图1：当四边形ABCD是正方形时，作出将△ADF绕点A顺时针旋转90度后的图形△ABM；并判断点M、B、C三点是否在同一条直线上是（填是或否）；
（2）如图1：当四边形ABCD是正方形时，且∠EAF=45°，请直接写出线段EF、BE、DF三者之间的数量关系EF=BE+DF；
（3）如图2：当AB=AD，∠B=∠D=90°，∠EAF是∠BAD的一半，问：（2）中的数量关系是否还存在，并说明理由；
（4）在（3）的条件下，将点E平移到BC的延长线上，请在图3中补全图形，并写出EF、BE、DF的关系．
13．计算或化简：
（1）（-$\frac{1}{2}$）0+（-2）3+（$\frac{1}{2}$）-1+2            
（2）2m•m2+（2m3）2÷m3
（3）（x+1）2-（-x-2）（-x+2）
（4）（2a-b+3）（2a+b-3）
20．从2开始，连续的偶数相加，它们和的情况如下表：
加数的个数（n）和　（S）
12=1×2
22+4=6=2×3
32+4+6=12=3×4
42+4+6+8=20=4×5
52+4+6+8+10=30=5×6
…　　　　…
（1）若n=8时，则S的值为72．
（2）根据表中的规律猜想：用n的式子表示S的公式为：S=2+4+6+8+…+2n=n（n+1）．
（3）根据上题的规律计算2+4+6+8+10+…+98+100的值．
10．计算：$\sqrt{8}$-|2$\sqrt{2}$-2|-π0+（$\frac{1}{2}$）-2=5．
17．化简求值：[（x+y）2-（x+2y）（x-2y）]÷y，其中x=-1，y=1．
14．给出下列命题：
①平行四边形的对角线互相平分；
②对角线互相平分的四边形是平行四边形；
③菱形的对角线互相垂直；
④对角线互相垂直的四边形是菱形．
其中真命题的个数为（　　）
A．1个B．2个C．3个D．4个
15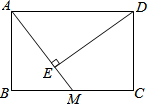．如图，在矩形ABCD中，AB=1，BC=$\frac{5}{2}$，M为BC中点，连接AM，过D作DE⊥AM于E，则DE的长度为（　　）
A．1B．$\frac{3\sqrt{13}}{13}$C．$\frac{10\sqrt{41}}{41}$D．$\frac{\sqrt{41}}{10}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网