题目内容
1.已知在四边形ABCD中,点E、F分别是BC、CD边上的一点.(1)如图1:当四边形ABCD是正方形时,作出将△ADF绕点A顺时针旋转90度后的图形△ABM;并判断点M、B、C三点是否在同一条直线上是(填是或否);
(2)如图1:当四边形ABCD是正方形时,且∠EAF=45°,请直接写出线段EF、BE、DF三者之间的数量关系EF=BE+DF;
(3)如图2:当AB=AD,∠B=∠D=90°,∠EAF是∠BAD的一半,问:(2)中的数量关系是否还存在,并说明理由;
(4)在(3)的条件下,将点E平移到BC的延长线上,请在图3中补全图形,并写出EF、BE、DF的关系.

分析 (1)首先由旋转的性质,画出旋转后的图形,然后由∠ABM=∠D=∠ABC=90°,证得点M、B、C三点共线;
(2)首先由旋转的性质可得:AM=AF,∠BAM=∠DAF,BM=DF,然后由∠EAF=45°,证得∠EAM=∠EAF,继而证得△EAM≌△EAF,继而证得结论;
(3)首先延长CB到P使BP=DF,证得△ABP≌△ADF(SAS),再证得△APE≌△AFE(SAS),继而证得结论;
(4)首先在BC上截取BP=DF,证得△ABP≌△ADF(SAS),再证得△APE≌△AFE(SAS),即可得EF=BE-BP=BE-DF.
解答 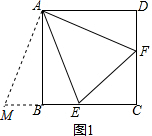 (1)解:如图1:
(1)解:如图1:
根据旋转的性质,∠ABM=90°,
∵四边形ABCD是正方形,
∴∠ABC=90°,
∴M、B、C三点在一条直线上.
故答案为:是;
(2)由旋转的性质可得:AM=AF,∠BAM=∠DAF,BM=DF,
∵四边形ABCD是正方形,∠EAF=45°,
∴∠DAF+∠BAE=45°,
∴∠EAM=∠BAM+∠BAE=45°,
∴∠EAM=∠EAF,
在△EAM和△EAF中,
$\left\{\begin{array}{l}{AM=AF}\\{∠EAM=∠EAF}\\{AE=AE}\end{array}\right.$,
∴△EAM≌△EAF(SAS),
∴EF=EM=BM+BE=BE+DF;
故答案为:EF=BE+DF;
(3)存在
理由如下:延长CB到P使BP=DF,
∵∠B=∠D=90°,
∴∠ABP=90°,
∴∠ABP=∠D,
在△ABP和△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠ABP=∠D}\\{BP=DF}\end{array}\right.$,
∴△ABP≌△ADF(SAS),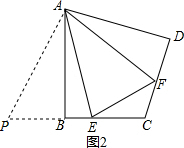 ∴AP=AF,∠BAP=∠DAF,
∴AP=AF,∠BAP=∠DAF,
∵∠EAF=$\frac{1}{2}$∠BAD,
∴∠BAE+∠DAF=∠EAF,
∴∠BAP+∠FAD=∠EAF,
即:∠EAP=∠EAF,
在△APE和△AFE中,
$\left\{\begin{array}{l}{AP=AF}\\{∠EAP=∠FAE}\\{AE=AE}\end{array}\right.$,
∴△APE≌△AFE(SAS),
∴PE=FE,
∴EF=BE+DF;
(4)如图3,补全图形.
证明:在BC上截取BP=DF,
∵∠B=∠ADC=90°,
∴∠ADF=90°,
∴∠B=∠ADF,
在△ABP和△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠B=∠ADF}\\{BP=DF}\end{array}\right.$,
∴△ABP≌△ADF(SAS),
∴AP=AF,∠BAP=∠DAF,
∵∠EAF=$\frac{1}{2}$∠BAD,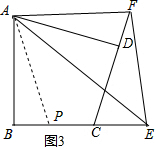
∴∠DAE+∠DAF=$\frac{1}{2}$∠BAD,
∴∠BAP+∠EAD=$\frac{1}{2}$∠BAD,
∴∠EAP=$\frac{1}{2}$∠BAD=∠EAF,
在△APE和△AFE中,
$\left\{\begin{array}{l}{AP=AF}\\{∠EAP=∠FAE}\\{AE=AE}\end{array}\right.$,
∴△APE≌△AFE(SAS),
∴PE=FE,
∴EF=BE-BP=BE-DF.
点评 此题属于四边形的综合题.考查了旋转的性质以及全等三角形的判定与性质.注意掌握旋转前后图形的对应关系,注意准确作出辅助线是解此题的关键.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 某学校为了解八年级学生的身体素质情况,随机抽取了八年级40名学生进行一分钟跳绳个数测试,以测试数据为样本,绘制出频数分布表和频数分布直方图,如图所示:
某学校为了解八年级学生的身体素质情况,随机抽取了八年级40名学生进行一分钟跳绳个数测试,以测试数据为样本,绘制出频数分布表和频数分布直方图,如图所示:八年级40名学生跳绳个数频数分布表
| 组别 | 分组/个 | 频数 |
| 第1组 | 80≤x<100 | 4 |
| 第2组 | 100≤x<120 | 8 |
| 第3组 | 120≤x<140 | m |
| 第4组 | 140≤x<160 | 12 |
| 第5组 | 160≤x<180 | 3 |
(1)表中的m=13;
(2)请把频数分布直方图补充完整;
(3)已知八年级学生一分钟跳绳个数的成绩标准是:x<120为不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.如果该年级有360名学生,根据以上信息,请你估算该年级跳绳不合格的人数约为108名,成绩为优的人数约为27名.
| A. | m=a+b,n=ab | B. | m=a+b,n=-ab | C. | m=-(a+b),n=ab | D. | m=-(a+b),n=-ab |

