题目内容
15.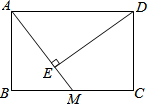 如图,在矩形ABCD中,AB=1,BC=$\frac{5}{2}$,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )
如图,在矩形ABCD中,AB=1,BC=$\frac{5}{2}$,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )| A. | 1 | B. | $\frac{3\sqrt{13}}{13}$ | C. | $\frac{10\sqrt{41}}{41}$ | D. | $\frac{\sqrt{41}}{10}$ |
分析 先求出△ADE的面积是矩形面积的一半,再用勾股定理求出AM,最后用面积公式求解即可.
解答 解:如图,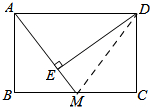
连结DM,
在矩形ABCD中,AB=1,BC=$\frac{5}{2}$,
∴S矩形ABCD=AB×BC=1×$\frac{5}{2}$=$\frac{5}{2}$,
∵M为BC中点,
∴S△ADM=$\frac{1}{2}$S矩形ABCD=$\frac{5}{4}$,
在RT△ABM中,AB=1,BM=$\frac{1}{2}$BC=$\frac{5}{4}$,
根据勾股定理得,AM=$\sqrt{A{B}^{2}+B{M}^{2}}$=$\frac{\sqrt{41}}{4}$,
∴S△ADM=$\frac{1}{2}$AM×DE=$\frac{1}{2}$×$\frac{\sqrt{41}}{4}$×DE=$\frac{5}{4}$,
∴DE=$\frac{10\sqrt{41}}{41}$,
故选C
点评 本题考查了矩形的性质,三角形的面积的计算,勾股定理,解本题的关键是判断△ADE的面积是矩形面积的一半.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
5.若(x-a)(x-b)=x2+mx+n,则m,n的值分别是( )
| A. | m=a+b,n=ab | B. | m=a+b,n=-ab | C. | m=-(a+b),n=ab | D. | m=-(a+b),n=-ab |
3.如图所示的四个图形中,( )不是正方体的表面展开图.
| A. |  | B. |  | C. |  | D. |  |
10. 如图,在△ABC中,AB=AC,D、E、F分别在三边上,且BE=CD,BD=CF,G为EF的中点,则∠DGE的度数是( )
如图,在△ABC中,AB=AC,D、E、F分别在三边上,且BE=CD,BD=CF,G为EF的中点,则∠DGE的度数是( )
 如图,在△ABC中,AB=AC,D、E、F分别在三边上,且BE=CD,BD=CF,G为EF的中点,则∠DGE的度数是( )
如图,在△ABC中,AB=AC,D、E、F分别在三边上,且BE=CD,BD=CF,G为EF的中点,则∠DGE的度数是( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
20.下列各组二次根式中是同类二次根式的是( )
| A. | $\sqrt{6}与\sqrt{24}$ | B. | $\sqrt{18}与\sqrt{\frac{1}{3}}$ | C. | $\sqrt{2}与\sqrt{12}$ | D. | $\sqrt{0.2}与\sqrt{27}$ |
4.在数轴上,一个点从-3开始向左移动1个单位长度,再向右移动2个单位长度得到点B,则点B表示的数是( )
| A. | +3 | B. | +1 | C. | -9 | D. | -2 |
