题目内容
20.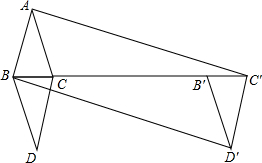 如图,△ABC中,AB=AC=3,BC=2,将△ABC沿BC翻折,得△DBC,再将△DBC沿射线BC方向平移k个距离得三角形D′B′C′,若四边形ABD′C′是矩形,则k=7.
如图,△ABC中,AB=AC=3,BC=2,将△ABC沿BC翻折,得△DBC,再将△DBC沿射线BC方向平移k个距离得三角形D′B′C′,若四边形ABD′C′是矩形,则k=7.
分析 过点D′作D′E⊥B′C′,垂足为E.首先求得EC′=1,然后证明△BAC′∽△C′ED′,从而可求得BC′=9,最后根据CC′=BC′-BC可求得平移的距离即k的值.
解答 解:如图所示:过点D′作D′E⊥B′C′,垂足为E.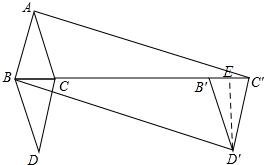
由翻折和平移的性质可知:B′D′=B′C′=3,B′C′=2,
∵B′D′=B′C′,D′E⊥B′C′,
∴EC′=$\frac{1}{2}B′C′$=1.
∵四边形ABD′C′是矩形,
∴∠AC′B+∠BC′D′=90°.
又∵∠BC′D+∠ED′C′=90°,
∴∠ED′C′=∠AC′B.
又∵∠BAC′=∠C′ED′,
∴△BAC′∽△C′ED′.
∴$\frac{AB}{BC′}=\frac{EC′}{C′D′}$即$\frac{3}{BC′}=\frac{1}{3}$.
∴BC′=9.
∴CC′=BC′-BC=9-2=7.
∴k=7.
故答案为:7.
点评 本题主要考查的是相似三角形的性质和判定、矩形的性质、等腰三角形的性质、翻折变换、平移变换,证得△BAC′∽△C′ED′是解题的关键.

练习册系列答案
相关题目
10.一水果经销商购进了A,B两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售(整箱配货),预计每箱水果的盈利情况如下表:
(1)如果按照“甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱”的方案配货,请你计算出经销商能盈利多少元?
(2)如果按照“甲、乙两店盈利相同配货”的方案配货,请写出一种配货方案:A种水果甲店2箱,乙店8箱;B种水果甲店6箱,乙店4箱,并根据你填写的方案计算出经销商能盈利多少元?
(3)在甲、乙两店各配货10箱,且保证乙店盈利不小于115元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少元?
| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 | 9元 | 13元 |
(2)如果按照“甲、乙两店盈利相同配货”的方案配货,请写出一种配货方案:A种水果甲店2箱,乙店8箱;B种水果甲店6箱,乙店4箱,并根据你填写的方案计算出经销商能盈利多少元?
(3)在甲、乙两店各配货10箱,且保证乙店盈利不小于115元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少元?
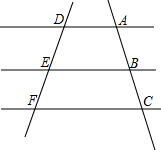 如图,已知AD∥EB∥FC,你能得到以下结论吗?说明理由.
如图,已知AD∥EB∥FC,你能得到以下结论吗?说明理由.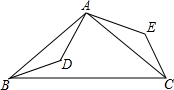 已知:AB=AC,AD=AE,BD=CE,求证:∠BAC=∠DAE.
已知:AB=AC,AD=AE,BD=CE,求证:∠BAC=∠DAE.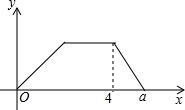 最近重庆八中学生宿舍在增修安全通道,一辆拉砖的货车从仓库匀速驶往学校,到达后用了1小时卸货,随即匀速返回.已知货车返回的速度是它从仓库驶往学饺的速度的2倍,货车离仓库的距离y(千米)关于时间x的函数图象如图所示.则a=4.5(小时).
最近重庆八中学生宿舍在增修安全通道,一辆拉砖的货车从仓库匀速驶往学校,到达后用了1小时卸货,随即匀速返回.已知货车返回的速度是它从仓库驶往学饺的速度的2倍,货车离仓库的距离y(千米)关于时间x的函数图象如图所示.则a=4.5(小时). 如图,⊙D与x轴相交于A(-2,0),B(-8,0),与y轴相切于C,则圆心D的坐标为(-5,4).
如图,⊙D与x轴相交于A(-2,0),B(-8,0),与y轴相切于C,则圆心D的坐标为(-5,4).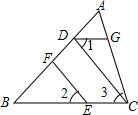 如图,EF⊥AB于F,CD⊥AB于D,点G在AC边上,且∠AGD=∠ACB,
如图,EF⊥AB于F,CD⊥AB于D,点G在AC边上,且∠AGD=∠ACB,
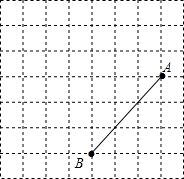 请在网格中建立平面直角坐标系,使得A点的坐标为(4,2).
请在网格中建立平面直角坐标系,使得A点的坐标为(4,2).