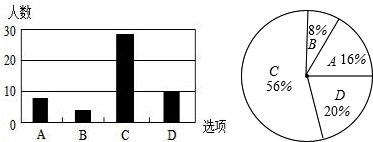
题目内容
12.解不等式组$\left\{\begin{array}{l}{\frac{x+6}{3}≥1①}\\{2-x>0②}\end{array}\right.$请你结合题意填空,完成本题的解答:(1)解不等式①,得x≥-3;
(2)解不等式②,得x<2;
(3)把不等式①和②的解集在数轴上表示出来:
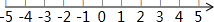
(4)原不等式组的解集为-3≤x<2.
分析 (1)根据不等式的基本性质求出即可;
(2)根据不等式的基本性质求出即可;
(3)把不等式的解集在数轴上表示出来即可;
(4)根据数轴即可得出答案.
解答 解:(1)解不等式①得:x≥-3,
故答案为:x≥-3;
(2)解不等式②得:x<2,
故答案为:x<2;
(3)在数轴上表示不等式①和②的解集为:
(4)原不等式组的解集为:-3≤x<2,
故答案为:-3≤x<2
点评 本题考查了解一元一次不等式组和解一元一次不等式的应用,能根据不等式的解集找出不等式组的解集是解此题的关键,难度适中.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
4. 实数a在数轴上的位置如图,则下列关系表示正确的是 ( )
实数a在数轴上的位置如图,则下列关系表示正确的是 ( )
 实数a在数轴上的位置如图,则下列关系表示正确的是 ( )
实数a在数轴上的位置如图,则下列关系表示正确的是 ( )| A. | a<1<-a | B. | a<-a<1 | C. | 1<-a<a | D. | -a<a<1 |

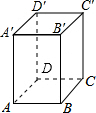 如图,正四棱柱的底面边长为4cm,侧棱长为8cm,一只蚂蚁从正四棱柱底面上的顶点A沿棱柱的表面到顶点C′处吃食物,那么蚂蚁走最短路线的路径为8$\sqrt{2}$cm.
如图,正四棱柱的底面边长为4cm,侧棱长为8cm,一只蚂蚁从正四棱柱底面上的顶点A沿棱柱的表面到顶点C′处吃食物,那么蚂蚁走最短路线的路径为8$\sqrt{2}$cm.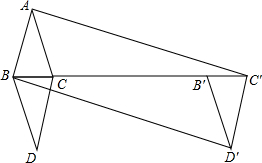 如图,△ABC中,AB=AC=3,BC=2,将△ABC沿BC翻折,得△DBC,再将△DBC沿射线BC方向平移k个距离得三角形D′B′C′,若四边形ABD′C′是矩形,则k=7.
如图,△ABC中,AB=AC=3,BC=2,将△ABC沿BC翻折,得△DBC,再将△DBC沿射线BC方向平移k个距离得三角形D′B′C′,若四边形ABD′C′是矩形,则k=7.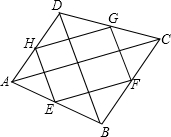 我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形,如图,E、F、G、H分别是四边形ABCD各边的中点,可证中点四边形EFGH是平行四边形,如果我们对四边形ABCD的对角线AC与BD添加一定的条件,则可使中点四边形EFGH成为特殊的平行四边形,请你经过探究后回答下面问题?
我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形,如图,E、F、G、H分别是四边形ABCD各边的中点,可证中点四边形EFGH是平行四边形,如果我们对四边形ABCD的对角线AC与BD添加一定的条件,则可使中点四边形EFGH成为特殊的平行四边形,请你经过探究后回答下面问题?