题目内容
17.若x0是方程ax2+2x+c=0(a≠0)的一个根,设M=1-ac,N=(ax0+1)2,则M与N的大小关系正确的为( )| A. | M>N | B. | M=N | C. | M<N | D. | 不确定 |
分析 把x0代入方程ax2+2x+c=0得ax02+2x0=-c,作差法比较可得.
解答 解:∵x0是方程ax2+2x+c=0(a≠0)的一个根,
∴ax02+2x0+c=0,即ax02+2x0=-c,
则N-M=(ax0+1)2-(1-ac)
=a2x02+2ax0+1-1+ac
=a(ax02+2x0)+ac
=-ac+ac
=0,
∴M=N,
故选:B.
点评 本题主要考查一元二次方程的解得概念及作差法比较大小,熟练掌握能使方程成立的未知数的值叫做方程的解是根本,利用作差法比较大小是解题的关键.

练习册系列答案
相关题目
8.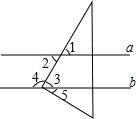 如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )
如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )
 如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )
如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )| A. | ∠2=60° | B. | ∠3=60° | C. | ∠4=120° | D. | ∠5=40° |
12. 已知实数a、b在数轴上对应的点如图所示,则下列式子正确的是( )
已知实数a、b在数轴上对应的点如图所示,则下列式子正确的是( )
 已知实数a、b在数轴上对应的点如图所示,则下列式子正确的是( )
已知实数a、b在数轴上对应的点如图所示,则下列式子正确的是( )| A. | a•b>0 | B. | a+b<0 | C. | |a|<|b| | D. | a-b>0 |
9.已知圆锥的母线长是12,它的侧面展开图的圆心角是120°,则它的底面圆的直径为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
7.在△ABC中,若∠A,∠B满足cosA=$\frac{\sqrt{3}}{2}$,∠B=45°,则∠C的大小是( )
| A. | 45° | B. | 60° | C. | 75° | D. | 105° |
 如图,BD是?ABCD的对角线,过点A作AE⊥BD,垂足为E,过点C作CF⊥BD,垂足为F.
如图,BD是?ABCD的对角线,过点A作AE⊥BD,垂足为E,过点C作CF⊥BD,垂足为F. 如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.