题目内容
2.为了了解某学校初四年级学生每周平均课外阅读时间的情况,随机抽查了该学校初四年级m名同学,对其每周平均课外阅读时间进行统计,绘制了如下条形统计图(图一)和扇形统计图(图二):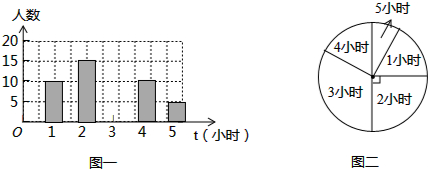
(1)根据以上信息回答下列问题:
①求m值.
②求扇形统计图中阅读时间为5小时的扇形圆心角的度数.
③补全条形统计图.
(2)直接写出这组数据的众数、中位数,求出这组数据的平均数.
分析 (1)①根据2小时所占扇形的圆心角的度数确定其所占的百分比,然后根据条形统计图中2小时的人数求得m的值;
②结合周角是360度进行计算;
③求得总人数后减去其他小组的人数即可求得第三小组的人数;
(2)利用众数、中位数的定义及平均数的计算公式确定即可.
解答 解:(1)①∵课外阅读时间为2小时的所在扇形的圆心角的度数为90°,
∴其所占的百分比为$\frac{90}{360}$=$\frac{1}{4}$,
∵课外阅读时间为2小时的有15人,
∴m=15÷$\frac{1}{4}$=60;
②依题意得:$\frac{5}{60}$×360°=30°;
③第三小组的频数为:60-10-15-10-5=20,
补全条形统计图为: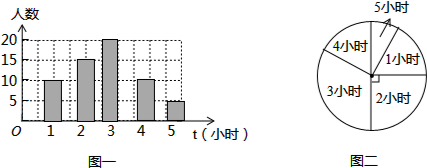
(2)∵课外阅读时间为3小时的20人,最多,
∴众数为 3小时;
∵共60人,中位数应该是第30和第31人的平均数,且第30和第31人阅读时间均为3小时,
∴中位数为3小时;
平均数为:$\frac{10×1+15×2+20×3+10×4+5×5}{60}$=2.75小时.
点评 本题考查了众数、中位数、平均数及扇形统计图和条形统计图的知识,解题的关键是能够结合两个统计图并找到进一步解题的有关信息,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.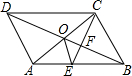 如图,?ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:
如图,?ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:
①∠ACD=30°;②S?ABCD=AC•BC;③OE:AC=$\sqrt{3}$:6;④S△OCF=2S△OEF
成立的个数有( )
 如图,?ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:
如图,?ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①∠ACD=30°;②S?ABCD=AC•BC;③OE:AC=$\sqrt{3}$:6;④S△OCF=2S△OEF
成立的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.设点A(a,b)是正比例函数y=-$\frac{3}{2}$x图象上的任意一点,则下列等式一定成立的是( )
| A. | 2a+3b=0 | B. | 2a-3b=0 | C. | 3a-2b=0 | D. | 3a+2b=0 |
17.若x0是方程ax2+2x+c=0(a≠0)的一个根,设M=1-ac,N=(ax0+1)2,则M与N的大小关系正确的为( )
| A. | M>N | B. | M=N | C. | M<N | D. | 不确定 |
7.若关于x的分式方程$\frac{2x-a}{x-2}=\frac{1}{2}$的解为非负数,则a的取值范围是( )
| A. | a≥1 | B. | a>1 | C. | a≥1且a≠4 | D. | a>1且a≠4 |
14.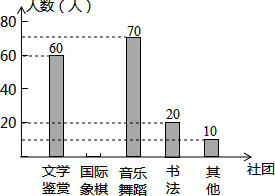 为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
根据统计图表的信息,解答下列问题:
(1)求本次抽样调查的学生总人数及a、b的值;
(2)将条形统计图补充完整;
(3)若该校共有1300名学生,试估计全校选择“音乐舞蹈”社团的学生人数.
 为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):| 选择意向 | 文学鉴赏 | 国际象棋 | 音乐舞蹈 | 书法 | 其他 |
| 所占百分比 | a | 20% | b | 10% | 5% |
(1)求本次抽样调查的学生总人数及a、b的值;
(2)将条形统计图补充完整;
(3)若该校共有1300名学生,试估计全校选择“音乐舞蹈”社团的学生人数.
11. 如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,折痕与AC边交于点E,分别过点D、E作BC的垂线,垂足为Q、P,称为第1次操作,记四边形DEPQ的面积为S1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,折痕与AC边交于点E1,分别过点D1、E1作BC的垂线,垂足为Q1、P1,称为第2次操作,记四边形D1E1P1Q1的面积为S2;按上述方法不断操作下去…,若△ABC的面积为1,则Sn的值为( )
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,折痕与AC边交于点E,分别过点D、E作BC的垂线,垂足为Q、P,称为第1次操作,记四边形DEPQ的面积为S1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,折痕与AC边交于点E1,分别过点D1、E1作BC的垂线,垂足为Q1、P1,称为第2次操作,记四边形D1E1P1Q1的面积为S2;按上述方法不断操作下去…,若△ABC的面积为1,则Sn的值为( )
 如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,折痕与AC边交于点E,分别过点D、E作BC的垂线,垂足为Q、P,称为第1次操作,记四边形DEPQ的面积为S1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,折痕与AC边交于点E1,分别过点D1、E1作BC的垂线,垂足为Q1、P1,称为第2次操作,记四边形D1E1P1Q1的面积为S2;按上述方法不断操作下去…,若△ABC的面积为1,则Sn的值为( )
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,折痕与AC边交于点E,分别过点D、E作BC的垂线,垂足为Q、P,称为第1次操作,记四边形DEPQ的面积为S1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,折痕与AC边交于点E1,分别过点D1、E1作BC的垂线,垂足为Q1、P1,称为第2次操作,记四边形D1E1P1Q1的面积为S2;按上述方法不断操作下去…,若△ABC的面积为1,则Sn的值为( )| A. | $\frac{{2}^{2n}-2}{{2}^{2n}}$ | B. | $\frac{{2}^{n}-1}{{2}^{2n-1}}$ | C. | $\frac{{3}^{n}-1}{{2}^{2n}}$ | D. | $\frac{{2}^{n-1}-1}{{2}^{2n}}$ |
12.若a>3,化简|a|-|3-a|的结果为( )
| A. | 3 | B. | -3 | C. | 2a-3 | D. | 2a+3 |