题目内容
 如图,已知△ABC,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )
如图,已知△ABC,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )| A、BD=CD |
| B、∠BAD=∠CAD |
| C、∠B=∠C |
| D、∠ADB=∠ADC |
考点:全等三角形的判定
专题:
分析:全等三角形的判定定理有SAS,ASA,SSS,AAS,直角三角形还有HL,根据定理逐个判断即可.
解答:解:因为AB=AC,AD=AD,
A、根据SSS即可推出△ABD≌△ACD,故本选项错误;
B、根据SAS即可推出△ABD≌△ACD,故本选项错误;
C、不符合全等三角形的判定定理,不能推出△ABD≌△ACD,故本选项正确;
D、根据∠ADB=∠ADC可得∠ADB=∠ADC=90°,然后根据HL即可推出△ABD≌△ACD,故本选项错误;
故选C.
A、根据SSS即可推出△ABD≌△ACD,故本选项错误;
B、根据SAS即可推出△ABD≌△ACD,故本选项错误;
C、不符合全等三角形的判定定理,不能推出△ABD≌△ACD,故本选项正确;
D、根据∠ADB=∠ADC可得∠ADB=∠ADC=90°,然后根据HL即可推出△ABD≌△ACD,故本选项错误;
故选C.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
能清楚的看出每个项目的具体数量的统计图是( )
| A、扇形统计图 |
| B、折线统计图 |
| C、条形统计图 |
| D、以上三种均可 |
下列四种说法中正确的是( )
①锐角的补角一定是钝角;②一个角的补角一定大于这个角;
③锐角和钝角互补; ④若两个角与同一个角互补,则这两个角相等.
①锐角的补角一定是钝角;②一个角的补角一定大于这个角;
③锐角和钝角互补; ④若两个角与同一个角互补,则这两个角相等.
| A、①② | B、①④ |
| C、①②④ | D、①②③④ |
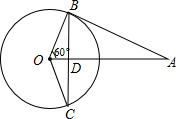 如图,AB与⊙O相切于点B,线段OA与弦BC垂直于点D,∠AOB=60°,BC=4cm,求切线AB的长.
如图,AB与⊙O相切于点B,线段OA与弦BC垂直于点D,∠AOB=60°,BC=4cm,求切线AB的长. 已知:点A、C分别是∠B的两条边上的点,点D、E分别是直线BA、BC上的点,直线AE、CD相交于点P点,D、E分别在线段BA、BC上.若∠B=60°,且AD=BE,BD=CE,求∠APD的度数.
已知:点A、C分别是∠B的两条边上的点,点D、E分别是直线BA、BC上的点,直线AE、CD相交于点P点,D、E分别在线段BA、BC上.若∠B=60°,且AD=BE,BD=CE,求∠APD的度数.