题目内容
抛物线y=x2+2x-3与x轴交于A、B两点,与y轴交于点C,对于下列结论:①y有最大值;②抛物线的对称轴是直线x=-1;③抛物线的顶点坐标是(-1,-4);④△ABC的面积是16;⑤当y<0时,x的取值范围是-3<x<1,其中正确结论的序号是 .
考点:抛物线与x轴的交点
专题:
分析:利用a>0,即可得出抛物线y=x2+2x-3,y有最小值,把抛物线的表达式用顶点式来表示即可得出抛物线的对称轴及顶点坐标,求出点AB的长即可得出△ABC的面积,求出点A,B的坐标即可得出当y<0时,x的取值范围.
解答:解:①∵a>0,
∴抛物线y=x2+2x-3,y有最小值,故①错误,
②∵y=x2+2x-3=(x+1)2-4,
∴抛物线的对称轴是直线x=-1;故②正确,
③∵y=x2+2x-3=(x+1)2-4,
∴抛物线的顶点坐标是(-1,-4);故③正确,
④∵抛物线y=x2+2x-3,
∴A(1,0),B(-3,0),
∴AB=4,
∴S△ABC=
×3×4=6,故④错误,
⑤∵A(1,0),B(-3,0),a>0
∴当y<0时,x的取值范围是-3<x<1,故⑤正确,
所以正确的是②③⑤.
故答案为:②③⑤.
∴抛物线y=x2+2x-3,y有最小值,故①错误,
②∵y=x2+2x-3=(x+1)2-4,
∴抛物线的对称轴是直线x=-1;故②正确,
③∵y=x2+2x-3=(x+1)2-4,
∴抛物线的顶点坐标是(-1,-4);故③正确,
④∵抛物线y=x2+2x-3,
∴A(1,0),B(-3,0),
∴AB=4,
∴S△ABC=
| 1 |
| 2 |
⑤∵A(1,0),B(-3,0),a>0
∴当y<0时,x的取值范围是-3<x<1,故⑤正确,
所以正确的是②③⑤.
故答案为:②③⑤.
点评:本题主要考查了抛物线与x轴的交点,解题的关键是熟记抛物线的性质.

练习册系列答案
相关题目
 如图,已知△ABC,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )
如图,已知△ABC,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )| A、BD=CD |
| B、∠BAD=∠CAD |
| C、∠B=∠C |
| D、∠ADB=∠ADC |
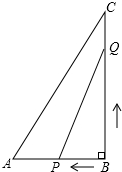 如图所示,在Rt△ABC中,∠B=90°,AB=6,BC=12,点P从点B开始沿BA边以1厘米/秒的速度向A移动;同时,点Q也从点B开始沿BC边以2厘米/秒的速度向点C移动.问:几秒后△PBQ的面积为24平方厘米?(结果用最简二次根式表示)
如图所示,在Rt△ABC中,∠B=90°,AB=6,BC=12,点P从点B开始沿BA边以1厘米/秒的速度向A移动;同时,点Q也从点B开始沿BC边以2厘米/秒的速度向点C移动.问:几秒后△PBQ的面积为24平方厘米?(结果用最简二次根式表示)
 将一个边长为1的正方形按如图所示的方法进行分割:部分①是整个正方形面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,…,依此类推,通过计算此图形中部分①、部分②、部分③…的面积之和,可得到式子
将一个边长为1的正方形按如图所示的方法进行分割:部分①是整个正方形面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,…,依此类推,通过计算此图形中部分①、部分②、部分③…的面积之和,可得到式子 如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…,第n行有n个点…,若该三角点阵前n行的点数和为300,则n的值为( )
如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…,第n行有n个点…,若该三角点阵前n行的点数和为300,则n的值为( )