题目内容
 已知:点A、C分别是∠B的两条边上的点,点D、E分别是直线BA、BC上的点,直线AE、CD相交于点P点,D、E分别在线段BA、BC上.若∠B=60°,且AD=BE,BD=CE,求∠APD的度数.
已知:点A、C分别是∠B的两条边上的点,点D、E分别是直线BA、BC上的点,直线AE、CD相交于点P点,D、E分别在线段BA、BC上.若∠B=60°,且AD=BE,BD=CE,求∠APD的度数.考点:全等三角形的判定与性质
专题:
分析:连结AC,由条件可以得出△ABC为等边三角形,再由等边三角形的性质就可以得出△CBD≌△ACE就可以得出∠BCD=∠CAE,就可以得出结论;
解答: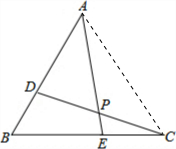 解:连结AC,
解:连结AC,
∵AD=BE,BD=CE,
∴AD+BD=BE+CE,
∴AB=BC.
∵∠B=60°,
∴△ABC为等边三角形.
∴∠B=∠ACB=60°,BC=AC.
在△CBD和△ACE中
,
∴△CBD≌△ACE(SAS),
∴∠BCD=∠CAE.
∵∠APD=∠CAE+∠ACD,
∴∠APD=∠BCD+∠ACD=60°.
 解:连结AC,
解:连结AC,∵AD=BE,BD=CE,
∴AD+BD=BE+CE,
∴AB=BC.
∵∠B=60°,
∴△ABC为等边三角形.
∴∠B=∠ACB=60°,BC=AC.
在△CBD和△ACE中
|
∴△CBD≌△ACE(SAS),
∴∠BCD=∠CAE.
∵∠APD=∠CAE+∠ACD,
∴∠APD=∠BCD+∠ACD=60°.
点评:此题考查了全等三角形的判定与性质的运用,等边三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
数轴上的点A表示的数是-1,将点A向左移动5个单位,终点表示的数是( )
| A、4 | B、-4 | C、6 | D、-6 |
 如图,已知△ABC,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )
如图,已知△ABC,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )| A、BD=CD |
| B、∠BAD=∠CAD |
| C、∠B=∠C |
| D、∠ADB=∠ADC |
 下图描述了小丽散步过程中离家的距离s(米)与散步所用时间t(分)之间的函数关系.依据图象,下面描述符合小红散步情景的是( )
下图描述了小丽散步过程中离家的距离s(米)与散步所用时间t(分)之间的函数关系.依据图象,下面描述符合小红散步情景的是( )| A、从家出发,到了一个公共阅报栏,看了一会儿报,就回家了 |
| B、从家出发,到了一个公共阅报栏,看了一会儿报后,继续向前走了一段,然后回家了 |
| C、从家出发,一直散步(没有停留),然后回家了 |
| D、从家出发,散了一会儿步,就找同学去了,18分钟后才开始返回 |
 如图所示,为某城市的街道平面图,图中的线段表示道路.
如图所示,为某城市的街道平面图,图中的线段表示道路.