题目内容
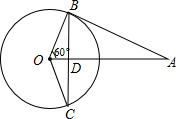 如图,AB与⊙O相切于点B,线段OA与弦BC垂直于点D,∠AOB=60°,BC=4cm,求切线AB的长.
如图,AB与⊙O相切于点B,线段OA与弦BC垂直于点D,∠AOB=60°,BC=4cm,求切线AB的长.考点:切线的性质
专题:
分析:由切线的性质可求得∠BAO=30°,在Rt△ABD中可求得BD,可得出AB=2BD,可求得AB.
解答:解:∵AB是⊙O的切线,
∴∠OBA=90°,
∵∠AOB=60°,
∴∠BAO=30°,
∵OA⊥BC,BC=4,
∴BD=2,
∴AB=2BD=4(cm).
∴∠OBA=90°,
∵∠AOB=60°,
∴∠BAO=30°,
∵OA⊥BC,BC=4,
∴BD=2,
∴AB=2BD=4(cm).
点评:本题主要考查切线的性质及直角三角形的性质,根据切线的性质得到∠BAO=30°是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
小红家的冰箱冷藏室温度是3℃,冷冻室的温度是-1℃,则她家的冰箱冷藏室比冷冻室温度高( )
| A、4℃ | B、-4℃ |
| C、2℃ | D、-2℃ |
 如图,已知△ABC,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )
如图,已知△ABC,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )| A、BD=CD |
| B、∠BAD=∠CAD |
| C、∠B=∠C |
| D、∠ADB=∠ADC |

 如图所示,为某城市的街道平面图,图中的线段表示道路.
如图所示,为某城市的街道平面图,图中的线段表示道路. 如图所示,在Rt△ABC中,∠B=90°,AB=6,BC=12,点P从点B开始沿BA边以1厘米/秒的速度向A移动;同时,点Q也从点B开始沿BC边以2厘米/秒的速度向点C移动.问:几秒后△PBQ的面积为24平方厘米?(结果用最简二次根式表示)
如图所示,在Rt△ABC中,∠B=90°,AB=6,BC=12,点P从点B开始沿BA边以1厘米/秒的速度向A移动;同时,点Q也从点B开始沿BC边以2厘米/秒的速度向点C移动.问:几秒后△PBQ的面积为24平方厘米?(结果用最简二次根式表示) 如同,△ABC是等边三角形,BD平分∠ABC,DE∥BC,则△ADE是什么三角形?AE与AB的大小有什么关系?为什么?
如同,△ABC是等边三角形,BD平分∠ABC,DE∥BC,则△ADE是什么三角形?AE与AB的大小有什么关系?为什么?