题目内容
17．
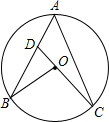如图，点A、B、C在⊙O上，CO的延长线交AB于点D，BD=BO，∠A=50°，则∠B的度数为（ ）| A． | 15° | B． | 20° | C． | 25° | D． | 30° |
分析 利用圆周角定理得到∠BOC的度数；然后结合等腰三角形的性质、邻补角的定义以及三角形内角和定理来求角B的度数．
解答 解：∵∠A=50°，
∴∠BOC=2∠A=100°，
∴∠BOD=80°．
又∵BD=BO，
∴∠BDO=∠BOD=80°
∴∠B=180°-80°-80°=20°．
故选：B．
点评 本题考查了圆周角定理，理清圆心角和圆周角的数量关系是解题的关键．
练习册系列答案
相关题目
8．
如图，AC是⊙O的弦，OF⊥AC于点F，延长OF，与过点A的切线交于点P，若∠P=30°，AP=$\sqrt{3}$，则OF的值是（ ）
如图，AC是⊙O的弦，OF⊥AC于点F，延长OF，与过点A的切线交于点P，若∠P=30°，AP=$\sqrt{3}$，则OF的值是（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{\sqrt{3}}{2}$ | D． | $\sqrt{3}$ |
5．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
12．
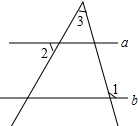如图，直线a∥b，∠1=110°，∠2=50°，则∠3的度数为（ ）
如图，直线a∥b，∠1=110°，∠2=50°，则∠3的度数为（ ）| A． | 50° | B． | 60° | C． | 70° | D． | 110° |
9．若正比例函数y=kx的图象经过点（2，-6），则k的值为（ ）
| A． | -3 | B． | -$\frac{1}{3}$ | C． | 3 | D． | $\frac{1}{3}$ |
7．某品牌运动鞋销售商在进行市场占有率的调查时，他最关注的是（ ）
| A． | 运动鞋型号的平均数 | B． | 运动鞋型号的众数 | ||
| C． | 运动鞋型号的中位数 | D． | 运动鞋型号的极差 |