题目内容
14. 一辆货车从甲地开往乙地,一辆客车从乙地开往甲地,客车先出发45分钟后,货车出发.如图是货车和客车离甲地的距离y货、y客(km)与货车行驶的时间x(h)之间的函数关系图象,根据图象回答下列问题:
一辆货车从甲地开往乙地,一辆客车从乙地开往甲地,客车先出发45分钟后,货车出发.如图是货车和客车离甲地的距离y货、y客(km)与货车行驶的时间x(h)之间的函数关系图象,根据图象回答下列问题:(1)直接写出:甲、乙两地相距300km,货车比客车晚2h到达终点
(2)货车出发几小时两车相遇?
(3)客车出发几小时,两车相距100km?
分析 (1)由图象可知,甲乙两地距离为300km,货车比客车晚2小时到达终点.
(2)可以用待定系数法,求出Y客车,Y货车的解析式.
(3)利用方程解决此类问题.
解答 解:(1)由图象可知:甲、乙两地相距 300km,货车比客车晚 2h到达终点.
(2)由题意:客车的速度=$\frac{300}{3+\frac{3}{4}}$=80km/h,
∴先走了80×$\frac{3}{4}$=60km,
∴Y客车的图象经过点(0,240),(3,0),设Y客=KX+b,
由题意:$\left\{\begin{array}{l}{b=240}\\{3K+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-80}\\{b=240}\end{array}\right.$,
则Y客=-80x+240,
易知:Y货=60X,
由:$\left\{\begin{array}{l}{Y=60X}\\{Y=-80X+240}\end{array}\right.$得到:$\left\{\begin{array}{l}{X=\frac{12}{7}}\\{Y=\frac{720}{7}}\end{array}\right.$,
故货车出发$\frac{12}{7}$小时与客车相遇.
(3)设客车出发X小时,两车相距100km.
由题意:-80X+240-60X=100或60X-(-80X+240)=100,
解得X=1或$\frac{17}{7}$,
∴1+$\frac{3}{4}=\frac{7}{4}$,$\frac{17}{7}+\frac{3}{4}=\frac{89}{28}$,
∴客车出发1或$\frac{89}{28}$小时,两车相距100km.
点评 本题考查的是用一次函数解决实际问题,此类题解决的关键是待定系数法求一次函数,结合方程的思想解决问题.

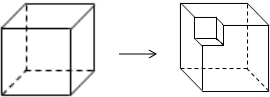 如图,从一个棱长为3cm的正方体的一顶点处挖去一个棱长为1cm的正方体,则剩余部分的体积和表面积分别是( )
如图,从一个棱长为3cm的正方体的一顶点处挖去一个棱长为1cm的正方体,则剩余部分的体积和表面积分别是( )| A. | 27cm3,54cm2 | B. | 26cm3,54cm2 | C. | 27cm3,51cm2 | D. | 26cm3,51cm2 |
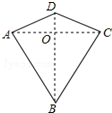 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,小明在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=$\frac{1}{2}$AC;③△ABD≌△CBD,其中正确的结论有( )
两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,小明在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=$\frac{1}{2}$AC;③△ABD≌△CBD,其中正确的结论有( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
| A. | 3 | B. | -7 | C. | 7 | D. | 0 |
| A. | 5x2+3x=8x3 | B. | 6x2•3x=18x2 | C. | (-6x2)3=-36x6 | D. | 6x2÷3x=2x |

