题目内容
 如图,⊙O是△ABC的外接圆,AB是直径,OD∥AC,且∠CBD=∠BAC,OD交⊙O于点E,交BC于F.
如图,⊙O是△ABC的外接圆,AB是直径,OD∥AC,且∠CBD=∠BAC,OD交⊙O于点E,交BC于F.(1)求证:BD是⊙O的切线;
(2)①若点E为OD的中点,则以O、A、C、E为顶点的四边形是
②若点E为弧BC的中点,AB=4,BD=3,求BC的长.
考点:切线的判定
专题:证明题
分析:(1)由AB是直径得∠ACB=90°,则∠BAC+∠ABC=90°,加上∠CBD=∠BAC,则∠CBD+∠ABC=90°,即∠ABD=90°,于是根据切线的判定定理即可得到结论;
(2)①连结CE、BE,如图,根据直角三角形斜边上的中线性质,由点E为OD的中点得到BE=OE=DE,则可判断△OBE为等边三角形,得到∠BOE=60°,利用OD∥AC得∠A=∠BOE=60°,又可判断△OAC为等边三角形,则∠ACO=60°,AC=AO,再利用AC∥OD得到∠ACO=∠COE=60°,可判断△OCE为等边三角形,则OE=CE,所以OA=OE=CE=AC,于是根据菱形的判定方法即可得到四边形AOEC为菱形;
②根据垂径定理,由点E为弧BC的中点得到OD⊥BC,则BF=CF,利用勾股定理计算出OD=
,再利用面积法计算出BF,然后利用BC=2BF进行计算.
(2)①连结CE、BE,如图,根据直角三角形斜边上的中线性质,由点E为OD的中点得到BE=OE=DE,则可判断△OBE为等边三角形,得到∠BOE=60°,利用OD∥AC得∠A=∠BOE=60°,又可判断△OAC为等边三角形,则∠ACO=60°,AC=AO,再利用AC∥OD得到∠ACO=∠COE=60°,可判断△OCE为等边三角形,则OE=CE,所以OA=OE=CE=AC,于是根据菱形的判定方法即可得到四边形AOEC为菱形;
②根据垂径定理,由点E为弧BC的中点得到OD⊥BC,则BF=CF,利用勾股定理计算出OD=
| 13 |
解答:(1)证明:∵AB是直径,
∴∠ACB=90°,
∴∠BAC+∠ABC=90°,
∵∠CBD=∠BAC,
∴∠CBD+∠ABC=90°,
即∠ABD=90°,
∴AB⊥BD,
∴BD是⊙O的切线;
(2)解:①连结CE、BE,如图,
∵点E为OD的中点,
∴BE=OE=DE,
∵OB=OE,
∴△OBE为等边三角形,
∴∠BOE=60°,
∵OD∥AC,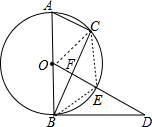
∴∠A=∠BOE=60°,
而OA=OC,
∴△OAC为等边三角形,
∴∠ACO=60°,AC=AO,
∵AC∥OD,
∴∠ACO=∠COE=60°,
∴△OCE为等边三角形,
∴OE=CE,
∴OA=OE=CE=AC,
∴四边形AOEC为菱形;
故答案为菱形;
②∵点E为弧BC的中点,
∴OD⊥BC,
∴BF=CF,
在Rt△OBD中,∵OB=2,BD=3,
∴OD=
=
,
∵
BF•OD=
OB•BD,
∴BF=
=
,
∴BC=2BF=
.
∴∠ACB=90°,
∴∠BAC+∠ABC=90°,
∵∠CBD=∠BAC,
∴∠CBD+∠ABC=90°,
即∠ABD=90°,
∴AB⊥BD,
∴BD是⊙O的切线;
(2)解:①连结CE、BE,如图,
∵点E为OD的中点,
∴BE=OE=DE,
∵OB=OE,
∴△OBE为等边三角形,
∴∠BOE=60°,
∵OD∥AC,

∴∠A=∠BOE=60°,
而OA=OC,
∴△OAC为等边三角形,
∴∠ACO=60°,AC=AO,
∵AC∥OD,
∴∠ACO=∠COE=60°,
∴△OCE为等边三角形,
∴OE=CE,
∴OA=OE=CE=AC,
∴四边形AOEC为菱形;
故答案为菱形;
②∵点E为弧BC的中点,
∴OD⊥BC,
∴BF=CF,
在Rt△OBD中,∵OB=2,BD=3,
∴OD=
| OB2+BD2 |
| 13 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴BF=
| 2×3 | ||
|
6
| ||
| 13 |
∴BC=2BF=
12
| ||
| 13 |
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了勾股定理、等边三角形的判定与性质和菱形的判定.

练习册系列答案
相关题目
下列是方程5x2-x=6的解的是( )
| A、x=1 | B、x=-1 |
| C、x=-2 | D、x=2 |
 如图点C是线段BD上一点,分别以BC和CD为一边,在BD的同侧作等边△ABC和等边△ECD,AC交BE于点G,CE交AD于点F.
如图点C是线段BD上一点,分别以BC和CD为一边,在BD的同侧作等边△ABC和等边△ECD,AC交BE于点G,CE交AD于点F.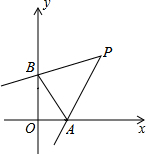 如图,在直角坐标系中,点P(2,2),∠P=45°,∠P的两边分别交坐标轴于A、B两点,则三角形OAB的周长是
如图,在直角坐标系中,点P(2,2),∠P=45°,∠P的两边分别交坐标轴于A、B两点,则三角形OAB的周长是 如图,将右边的图案变成左边的图案,是通过
如图,将右边的图案变成左边的图案,是通过 如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=a,且sinα=
如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=a,且sinα=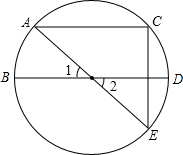 如图,直径AE,BD交于点O,点D为
如图,直径AE,BD交于点O,点D为
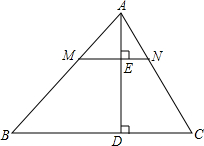 如图,AD是△ABC的高,点M在AB边上,点N在AC边上,MN⊥AD,垂足为E.下列说法正确的是
如图,AD是△ABC的高,点M在AB边上,点N在AC边上,MN⊥AD,垂足为E.下列说法正确的是 在如图所示的方格纸中,按下列要求画图:
在如图所示的方格纸中,按下列要求画图: