题目内容
20.已知△ABC和△DEF相似,且相似比为2:3,则△ABC与△DEF的周长之比为2:3.分析 根据相似三角形(多边形)的周长的比等于相似比求解.
解答 解:∵△ABC与△DEF的相似比为2:3,
∴它们的周长比为2:3.
故答案为2:3.
点评 本题考查了相似三角形的性质:相似三角形的对应角相等,对应边的比相等.相似三角形(多边形)的周长的比等于相似比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.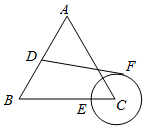 如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )
如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )
 如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )
如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )| A. | 有最大值,无最小值 | B. | 有最小值,无最大值 | ||
| C. | 有最大值,也有最小值 | D. | 为定值 |
7.下列说法正确的是( )
| A. | 两个矩形一定相似 | B. | 两个菱形一定相似 | ||
| C. | 两个等腰三角形一定相似 | D. | 两个等边三角形一定相似 |
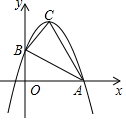 如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y铀的交点为B(0,3),其顶点为C,对称轴为x=1.
如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y铀的交点为B(0,3),其顶点为C,对称轴为x=1.