题目内容
5．如果关于x的一元二次方程x2+px+q=0的两根分别为x1=3、x2=1，那么这个一元二次方程是x2-4x+3=0．分析 由根与系数的关系求得p，q的值．
解答 解：方程两根分别为x1=3，x2=1，
则x1+x2=-p=3+1=4，x1x2=q=3
∴p=-4，q=3，
∴原方程为x2-4x+3=0．
故答案为x2-4x+3=0．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．也考查了一元二次方程的解．
练习册系列答案
名校课堂系列答案
相关题目
13．关于抛物线y=ax2和y=-ax2（a≠0），给出下列说法：
①两条抛物线都关于x轴对称；
②两条抛物线都关于原点对称；
③两条抛物线各自关于y轴对称；
④两条抛物线有公共的顶点．
其中正确的说法有（ ）
①两条抛物线都关于x轴对称；
②两条抛物线都关于原点对称；
③两条抛物线各自关于y轴对称；
④两条抛物线有公共的顶点．
其中正确的说法有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
10．
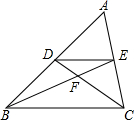如图，在△ABC中，D、E分别为AB、AC边上的点，DE∥BC，BE与CD相交于点F，则下列结论一定正确的是（ ）
如图，在△ABC中，D、E分别为AB、AC边上的点，DE∥BC，BE与CD相交于点F，则下列结论一定正确的是（ ）| A． | $\frac{DF}{FC}=\frac{AE}{AC}$ | B． | $\frac{AD}{AB}=\frac{EC}{AC}$ | C． | $\frac{AD}{DB}=\frac{DE}{BC}$ | D． | $\frac{DF}{BF}=\frac{EF}{FC}$ |
）
12．在数轴上距离原点2个单位长度的点所表示的数是（ ）
| A． | ±2 | B． | -2 | C． | 2 | D． | 4 |