题目内容
15.如图,Rt△ABC内接于⊙O,点E为弧BC中点,AD平分∠BAC交BC于D,连接AD、DE.(1)求证:∠ADB=∠CDE;
(2)AC交DE于H,且∠DHC=90°,连接BE分别交AD、AC于M、N,求证:BM=EN.
(3)在(1)的条件下,连接BE交AD于M,连接CM交DE于K,若CM⊥DE,若BD=2$\sqrt{10}$,求AM的长.

分析 (1)如图1中,延长AD交⊙O于F,连接OF.首先证明E、O、F共线,再证明∠EDO=∠FDO,由∠ADB=∠FDO即可证明.
(2)如图2中,连接AE,想办法证明△BAM≌△EAN即可解决问题.
(3)如图3中,连接AE、EC、BF.首先证明△EOD≌△COH,推出△BDM≌△EHM,BM=EM,再证明△BDM∽△CDE,推出$\frac{BD}{CD}$=$\frac{BM}{EC}$=$\frac{1}{2}$,求出CD,再由△FMB∽△EMA,
推出$\frac{BM}{BF}$=$\frac{AM}{AE}$=$\frac{1}{2}$,设AM=a,则AE=2a,EM=BM=$\sqrt{5}$a,BF=2$\sqrt{5}$a,FM=5a,在Rt△AFE中,根据AF2+AE2=EF2列出方程即可解决问题.
解答 (1)证明:如图1中,延长AD交⊙O于F,连接OF.
∵FA平分∠BAC,
∴∠FAB=∠FAC,
∴$\widehat{BF}$=$\widehat{CF}$,
∴OF⊥BC,
∵$\widehat{BE}$=$\widehat{EC}$,
∴EO⊥BC,
∴E、O、F共线,
∴DO垂直平分线段EF,
∴DE=DF,
∴∠ODE=∠ODF,
∵∠ADB=∠ODF,
∴∠ADB=∠CDE.
(2)证明:如图2中,连接AE.
∵AC⊥DE,
∴∠DHC=90°=∠DOE=90°,
∴∠C+∠CDH=90°,∠CDH+∠DEO=90°,
∴∠C=∠DEO=∠F,
∴$\widehat{AB}$=$\widehat{AE}$,
∴∠ABM=∠AEN,AB=AE,
∵∠BAM=$\frac{1}{2}$∠BOF=45°,∠EAN=$\frac{1}{2}$∠EOC=45°,
∴∠BAM=∠EAN,
∴△BAM≌△EAN,
∴BM=EN.
(3)解:如图3中,连接AE、EC、BF.
∵CM⊥DE,
∴∠CKD=90°=∠EOD,
∴∠DEO+∠EDO=90°,∠EDO+∠HCO=90°,
∵EO=CO,∠EOD=∠COH=90°,
∴△EOD≌△COH,
∴OD=OH,∠EDO=∠CHO=∠EHK=∠ADB,∵OB=OE,
∴BD=EH,∵∠DBM=∠HEM=45°,
∴△BDM≌△EHM,
∴BM=EM,
∵EB=EC,
∴EC=2BM,
∵∠DBM=∠ECD=45°,∠MDB=∠EDC,
∴△BDM∽△CDE,
∴$\frac{BD}{CD}$=$\frac{BM}{EC}$=$\frac{1}{2}$,∵BD=2$\sqrt{10}$,
∴CD=4$\sqrt{10}$,
∴BC=EF=6$\sqrt{10}$,
∵∠FBM=∠MAE=90°,∠FMB=AME,
∴△FMB∽△EMA,
∴$\frac{BM}{BF}$=$\frac{AM}{AE}$,
∵BF=BE=2BM,
∴$\frac{BM}{BF}$=$\frac{AM}{AE}$=$\frac{1}{2}$,设AM=a,则AE=2a,EM=BM=$\sqrt{5}$a,BF=2$\sqrt{5}$a,FM=5a,
∴AF=6a,
在Rt△AFE中,∵AF2+AE2=EF2,
∴(6a)2+(2a)2=(6$\sqrt{10}$)2,
∵a>0,
∴a=3,
∴AM=3.
点评 本题考查圆综合题、垂径定理、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是灵活应用全等三角形或相似三角形的性质解决问题,学会利用参数构建方程解决问题,属于中考压轴题.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案| A. | -10 | B. | 10 | C. | $\frac{2}{9}$ | D. | $\frac{2}{11}$ |
| A. | $\sqrt{2}$ | B. | $\sqrt{9}$ | C. | $\sqrt{18}$ | D. | $\sqrt{\frac{1}{3}}$ |
| A. | $\frac{2}{3}$ | B. | $\frac{8}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{8}{3}$ |
 有理数m、n在数轴上所对应的点的位置如图所示,则m+n的值( )
有理数m、n在数轴上所对应的点的位置如图所示,则m+n的值( )| A. | 大于0 | B. | 小于0 | C. | 等于0 | D. | 大于n |

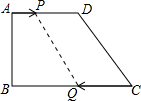 直角梯形ABCD中,∠B=90°,AD∥BC,AD=18cm,BC=21cm,点P从点A以1cm/s的速度向点D运动,同时点Q从点C以2cm/s的速度向点B运动.问:
直角梯形ABCD中,∠B=90°,AD∥BC,AD=18cm,BC=21cm,点P从点A以1cm/s的速度向点D运动,同时点Q从点C以2cm/s的速度向点B运动.问: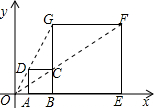 如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为$\frac{1}{3}$.点A、B、E在x轴上,若正方形BEFG的边长为6,则C点坐标为(3,2).
如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为$\frac{1}{3}$.点A、B、E在x轴上,若正方形BEFG的边长为6,则C点坐标为(3,2).