题目内容
8.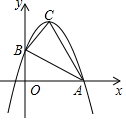 如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y铀的交点为B(0,3),其顶点为C,对称轴为x=1.
如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y铀的交点为B(0,3),其顶点为C,对称轴为x=1.(1)求抛物线的解析式;
(2)判断△ABC的形状;
(3)已知点M为线段AB上方抛物线上的一个动点,请写出△ABM面积关系式,并求出当△ABM面积最大时点M的坐标.
分析 (1)直接根据题意列出关于a、b、c的方程组,解方程组即可解决问题.
(2)通过计算证明:BC2+AB2=AC2,利用勾股定理的逆定理即可判断.
(3)如图,设M(m,-m2+2m+3)连接OM、MB、MA,根据S△ABM=S△OAM+S△OBM-S△AOB,构建二次函数,利用二次函数的性质即可解决问题.
解答 解:(1)由题意得:$\left\{\begin{array}{l}{9a+3b+c=0}\\{-\frac{b}{2a}=1}\\{c=3}\end{array}\right.$,
解该方程组得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为y=-x2+2x+3.
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴顶点C(1,4),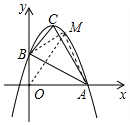
∵A(3,0),B(0,3),
∴AB=3$\sqrt{2}$,AC=2$\sqrt{5}$,BC=$\sqrt{2}$,
∵BC2+AB2=2+18=20,AC2=20,
∴BC2+AB2=AC2,
∴∠ABC=90°,
∴△ABC是直角三角形.
(3)如图,设M(m,-m2+2m+3)连接OM、MB、MA.
∵S△ABM=S△OAM+S△OBM-S△AOB,
∴S△ABM=$\frac{1}{2}$×3×(m+-m2+2m+3)-$\frac{9}{2}$=-$\frac{3}{2}$m2+$\frac{9}{2}$m=-$\frac{3}{2}$(m-$\frac{3}{2}$)2+$\frac{27}{8}$,
∵-$\frac{3}{2}$<0,
∴m=$\frac{3}{2}$时,△ABM面积的最大值为$\frac{27}{8}$.此时点M坐标($\frac{3}{2}$,$\frac{15}{4}$).
点评 本题考查二次函数的综合题、勾股定理的逆定理、两点间距离公式、三角形的面积等知识,解题的关键是灵活运用待定系数法确定函数解析式,学会构建二次函数,利用二次函数的性质解决最值问题,属于中考常考题型.

 名校课堂系列答案
名校课堂系列答案①两条抛物线都关于x轴对称;
②两条抛物线都关于原点对称;
③两条抛物线各自关于y轴对称;
④两条抛物线有公共的顶点.
其中正确的说法有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
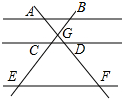 如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,那么$\frac{BC}{CE}$的值等于( )
如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,那么$\frac{BC}{CE}$的值等于( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
 ;
;  .
. 如图,在等边△ABC中,K、D两点分别在边AB、BC上,BK=CD,连接AD、CK,并延长CK至点F,连接FB,∠F=30°,若FC=11,CE=3时,则AE的长为5.
如图,在等边△ABC中,K、D两点分别在边AB、BC上,BK=CD,连接AD、CK,并延长CK至点F,连接FB,∠F=30°,若FC=11,CE=3时,则AE的长为5.

 )
)