题目内容
9.不等式$\frac{3x+1}{2}$-5≤3的正整数解的和为15.分析 首先解不等式,确定不等式的解集,然后确定解集中的正整数,最后求和即可.
解答 解:去分母,得:3x+1-10≤6,
移项,得3x≤6+10-1,
合并同类项,得3x≤15,
系数化成1得x≤5.
则正整数解是:1,2,3,4,5.
则和是:1+2+3+4+5=15.
故答案是:15.
点评 本题考查了不等式的解法,正确解不等式,求出解集是解答本题的关键.解不等式应根据不等式的基本性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.函数$y=\frac{1}{{\sqrt{x-1}}}$中自变量的取值范围是( )
| A. | x≠1 | B. | x>1 | C. | x≥1 | D. | x≥-1 |
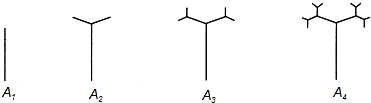
20.如图,如图是按照一定规律画出的“树形图”,经观察可以发现:图A2比图A1多出2个“树枝”,图A3比图A多出4个“树枝”,图A4比图A3多出8个“树枝”,…,照此规律,图A6比图A2多出“树枝”( )

| A. | 64 | B. | 60 | C. | 56 | D. | 32 |
17. 如图,在方格纸上有一个三角形ABC,则这个三角形是( )
如图,在方格纸上有一个三角形ABC,则这个三角形是( )
 如图,在方格纸上有一个三角形ABC,则这个三角形是( )
如图,在方格纸上有一个三角形ABC,则这个三角形是( )| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 不能确定 |
14.-$\frac{1}{3}$的倒数是( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -3 |
19.在平面直角坐标系中,先将抛物线y=x2+bx-c关于x轴作轴对称变换,再将所得的抛物线关于y轴作轴对称变换,那么经两次变换后所得的新抛物线的解析式为( )
| A. | y=x2+bx-c | B. | y=x2-bx+c | C. | y=-x2+bx+c | D. | y=-x2+bx-c |
