题目内容
2.如图1,抛物线y=ax2-3ax-4a(a<0)交x轴于点A、B(A左B右),交y轴正半轴于点C.(1)求A、B两点的坐标;
(2)点D在抛物线在第一象限的部分上一动点,当∠ACB=90°时,
①求抛物线的解析式;
②当四边形OCDB的面积最大时,求点D的坐标;
③如图2,若E为BC的中点,DE的延长线交线段AB于点F,当△BEF为钝角三角形时,请直接写出点D的纵坐标y的范围.

分析 (1)y=0,即可得到0=ax2-3ax-4a,从而得到A(-1,0),B(4,0);
(2)①根据射影定理得,CO2=A0•BO,即可得出结果;
②求出BC解析式,根据SOCDB=4+$\frac{1}{2}$×4×(-$\frac{1}{2}$x2+$\frac{3}{2}$x+2+$\frac{1}{2}$x-2)即可求出当四边形OCDB的面积最大时点D的坐标;
③分两种情况讨论:当90°<∠FEB<180°时,$\frac{13}{9}$<y<-4+$\sqrt{41}$;当90°<∠EFB<180°,2<y<3.
解答 解:(1)令y=0,则0=ax2-3ax-4a,
∴x=4,x=-1,
∴A(-1,0),B(4,0).
(2)①∵∠ACB=90°,CO⊥AB,
∴根据射影定理得,CO2=A0•BO,
∴CO=2,
∴-4a=2,
∴a=-$\frac{1}{2}$,
∴抛物线解析式y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2
②如图1,设BC解析式为y=kx+b,
把B(4,0),C(0,2)分别代入解析式得,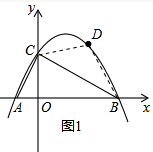
$\left\{\begin{array}{l}4k+b=0\\ b=2\end{array}\right.$,解得,$\left\{\begin{array}{l}k=-\frac{1}{2}\\ b=2\end{array}\right.$,
则BC解析式为y=-$\frac{1}{2}$x+2,设D(x,-$\frac{1}{2}$x2+$\frac{3}{2}$x+2),
∴SOCDB=4+$\frac{1}{2}$×4×(-$\frac{1}{2}$x2+$\frac{3}{2}$x+2+$\frac{1}{2}$x-2)=4-x2+4x,
∴当x=2,S最大,
∴D(2,3).
③如图2,
∵B(4,0),C(0,2),
∴点E的坐标为(2,1),
当FD⊥BC时,设FD解析式为y=2x+m,
将(2,1)代入解析式得,m=-3,
函数解析式为y=2x-3,
与y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2组成方程组得,
$\left\{\begin{array}{l}y=2x-3\\ y=-\frac{1}{2}{x}^{2}+\frac{3}{2}x+2\end{array}\right.$,
解得,y1=-4+$\sqrt{41}$,y2=-4-$\sqrt{41}$(舍去). 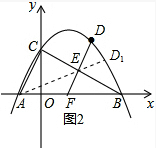
设AD1的解析式为y=sx+t,
将E(2,1)和A(-1,0)分别代入解析式得,
$\left\{\begin{array}{l}2s+t=1\\-s+t=0\end{array}\right.$,
解得,$\left\{\begin{array}{l}s=\frac{1}{3}\\ t=\frac{1}{3}\end{array}\right.$,
解析式为y=$\frac{1}{3}$x+$\frac{1}{3}$.
与y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2组成方程组得,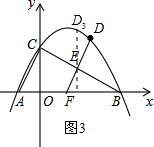
$\left\{\begin{array}{l}y=\frac{1}{3}x+\frac{1}{3}\\ y=-\frac{1}{2}{x}^{2}+\frac{3}{2}x+2\end{array}\right.$
解得,y3=0(舍去),y4=$\frac{13}{9}$.
当90°<∠FEB<180°时,$\frac{13}{9}$≤y<-4+$\sqrt{41}$;
如图3,D3E⊥x轴时,得D3(2,3),
当90°<∠EFB<180°时,2<y<$\frac{25}{8}$.
点评 本题考查了二次函数综合题,涉及待定系数法求一次函数解析式、二次函数解析式、二次函数最值、中点坐标公式,要注意数形结合求y的取值范围.

| A. | 3 | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -3 |
| A. | 77×105 | B. | 7.7×106 | C. | 7.7×105 | D. | 0.77×106 |
| A. | y=x2+bx-c | B. | y=x2-bx+c | C. | y=-x2+bx+c | D. | y=-x2+bx-c |
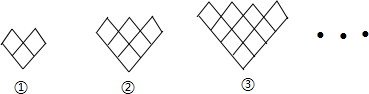
| A. | 36 | B. | 38 | C. | 34 | D. | 28 |
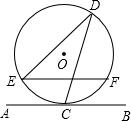 如图,如果直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长是( )
如图,如果直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长是( )| A. | 2$\sqrt{3}$ | B. | 8 | C. | 2$\sqrt{10}$ | D. | 2$\sqrt{13}$ |
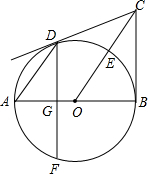 如图,AB是⊙O的直径,BC⊥AB于点B,连接OC、BD相交于点E,弦AD∥OC,弦DF⊥AB于点G.
如图,AB是⊙O的直径,BC⊥AB于点B,连接OC、BD相交于点E,弦AD∥OC,弦DF⊥AB于点G.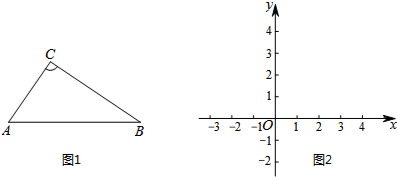
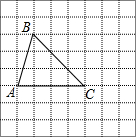 三角形ABC(记作△ABC)在8×8方格中,位置如图所示,A(-3,1),B(-2,4).
三角形ABC(记作△ABC)在8×8方格中,位置如图所示,A(-3,1),B(-2,4).