题目内容
9．在Rt△ABC中，∠C=90°，AB=10，AC=6，以C为圆心作⊙C和AB相切，则⊙C的半径长为4.8．分析 先根据题意画出图形，再结合切线的性质及勾股定理、三角形的面积公式解答．
解答 
解：设以C为圆心的圆与AB相切于点D，
根据切线的性质知，CD是圆C的半径，也是直角三角形斜边上的高，
由勾股定理知，BC=$\sqrt{{AB}^{2}{-AC}^{2}}$=8，
又S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD，代入各值，
解得：CD=4.8．
故答案为：4.8．
点评 本题利用了切线的性质和勾股定理、直角三角形的面积公式求解，注意根据题意画出图形以便于解题．
练习册系列答案
黄冈小状元同步计算天天练系列答案
相关题目
2．我市某中学举办了一次以“我的中国梦”为主题的演讲比赛，最后确定9名同学参加决赛，他们的决赛成绩各不相同，其中小辉已经知道自己的成绩，但能否进前5名，他还必须清楚这9名同学成绩的（ ）
| A． | 众数 | B． | 平均数 | C． | 中位数 | D． | 方差 |
19．在平面直角坐标系中，先将抛物线y=x2+bx-c关于x轴作轴对称变换，再将所得的抛物线关于y轴作轴对称变换，那么经两次变换后所得的新抛物线的解析式为（ ）
| A． | y=x2+bx-c | B． | y=x2-bx+c | C． | y=-x2+bx+c | D． | y=-x2+bx-c |
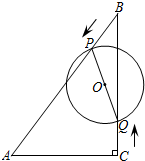如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点B出发，在BA边上以每秒5cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4cm的速度向点B匀速运动，运动时间为t秒（0≤t≤2），连接PQ，以PQ为直径作⊙O．
如图，菱形OABC的顶点O在坐标原点，顶点B在x轴的正半轴上，OA边所在直线为y=$\frac{\sqrt{3}}{3}$x，AB边所在直线为y=-$\frac{\sqrt{3}}{3}$x+2．