题目内容
1．用合适的方法解方程组：$\left\{\begin{array}{l}{3（x-1）=y+5}\\{5（y-1）=3（x+5）}\end{array}\right.$．分析 方程组整理后，利用加减消元法求出解即可．
解答 解：方程组整理得：$\left\{\begin{array}{l}{3x-y=8①}\\{3x-5y=-20②}\end{array}\right.$，
①-②得：4y=28，即y=7，
把y=7代入①得：x=5，
则方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=7}\end{array}\right.$．
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
相关题目
11．
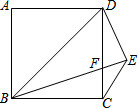如图，在正方形ABCD中，BD=BE，CE∥BD，BE交CD于F点，则∠DFE的度数为（ ）
如图，在正方形ABCD中，BD=BE，CE∥BD，BE交CD于F点，则∠DFE的度数为（ ）| A． | 45° | B． | 60° | C． | 75° | D． | 90° |
12．在0、-$\sqrt{3}$、-$\frac{2}{3}$、|-2|这四个数中，最小的数是（ ）
| A． | -$\sqrt{3}$ | B． | -$\frac{2}{3}$ | C． | 0 | D． | |-2| |
9．2-3的绝对值是（ ）
| A． | -8 | B． | ±8 | C． | $\frac{1}{8}$ | D． | -$\frac{1}{8}$ |
16．已知点M（1，a）和点N（2，b）是一次函数y=3x-1图象上的两点，则a与b的大小关系是（ ）
| A． | a＞b | B． | a=b | C． | a＜b | D． | 以上都不对 |
6．在一个不透明的口袋中装有大小相同的5个球，其中有3个白球，2个黑球．现每次取一个，无放回地抽取两次，则在第一次抽到白球的条件下，第二次抽到白球的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{3}{4}$ | C． | $\frac{3}{5}$ | D． | $\frac{1}{10}$ |
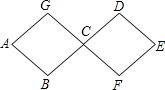如图，两个全等菱形的边长为1米，一个微型机器人由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动，行走2014米停下，则这个微型机器人所停的点是（ ）