题目内容
3.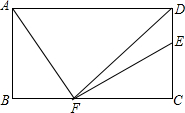 如图,矩形ABCD中,AD=12,AB=7,DF平分∠ADC,AF⊥EF.
如图,矩形ABCD中,AD=12,AB=7,DF平分∠ADC,AF⊥EF.(1)求EF的长;
(2)在平面上是否存在点Q,使得QA=QD=QE=QF?若存在,求出QA的长;若不存在,请说明理由.
分析 (1)由矩形的性质得出∠B=∠C=∠ADC=90°,AB=DC=7,BC=AD=12,证出△DCF是等腰直角三角形,得出FC=DC=7,由ASA证明△ABF≌△FCE,得出EF=AF,由勾股定理计算即可;
(2)存在;FE、AD的垂直平分线交于一点即点Q;连接AE、QF;证出FQ是Rt△AFE的中线,由直角三角形斜边上的中线定理得出FQ=QA=QE,再由等腰直角三角形的性质得出QE,即可得出QA.
解答 解:(1)∵四边形ABCD是矩形,
∴∠B=∠C=∠ADC=90°,AB=DC=7,BC=AD=12,
∴∠BAF+∠AFB=90°,
∵DF平分∠ADC,∴∠ADF=∠CDF=45°,
∴△DCF是等腰直角三角形,
∴FC=DC=7,
∴AB=FC,
∵AF⊥EF,
∴∠AFE=90°,
∴∠AFB+∠EFC=90°,
∴∠BAF=∠EFC,
在△ABF和△FCE中,
$\left\{\begin{array}{l}{∠BAF=∠EFC}&{\;}\\{AB=FC}&{\;}\\{∠B=∠C}&{\;}\end{array}\right.$,
∴△ABF≌△FCE(ASA),
∴EF=AF=$\sqrt{{7}^{2}+{5}^{2}}$=$\sqrt{74}$;
(2)存在;
FE、AD的垂直平分线交于一点即点Q;连接AE、QF;如图所示:
由(1)得:EF=AF,
∴△AEF是等腰直角三角形,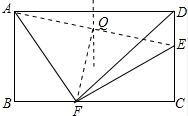 在Rt△AFE中,AQ=EQ,
在Rt△AFE中,AQ=EQ,
∴FQ是Rt△AFE的中线,
∴FQ=QA=QE,AF=EF=$\sqrt{74}$,
∴QE=$\frac{EF}{\sqrt{2}}$=$\sqrt{37}$,
∴QA=$\sqrt{37}$.
点评 本题考查了矩形的性质、等腰直角三角形的性质、全等三角形的判定与性质、勾股定理;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案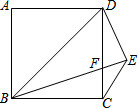 如图,在正方形ABCD中,BD=BE,CE∥BD,BE交CD于F点,则∠DFE的度数为( )
如图,在正方形ABCD中,BD=BE,CE∥BD,BE交CD于F点,则∠DFE的度数为( )| A. | 45° | B. | 60° | C. | 75° | D. | 90° |
(1)若该初中研训部认为工作态度、操作技能和学科知识同等重要,则谁将被聘用?
| 候选人 | 工作态度 | 操作技能 | 学科知识 |
| 甲 | 83 | 79 | 81 |
| 乙 | 74 | 83 | 82 |
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
| A. | -$\sqrt{3}$ | B. | -$\frac{2}{3}$ | C. | 0 | D. | |-2| |
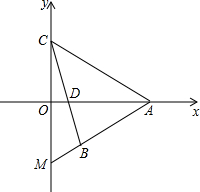 一次函数y=kx-4k交x轴正半轴于点A,交y轴正半轴于点C,当k变化时,作点C关于x轴对称的点M,CB交AM于B,交x轴于D,且2∠OCD=∠CAO,求AB+AC的值.
一次函数y=kx-4k交x轴正半轴于点A,交y轴正半轴于点C,当k变化时,作点C关于x轴对称的点M,CB交AM于B,交x轴于D,且2∠OCD=∠CAO,求AB+AC的值.