题目内容
19.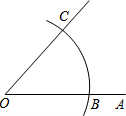 如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为( )
如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 根据作图的方法得出△OBC是等边三角形,进而利用特殊角的三角函数值求出答案.
解答  解:连接BC,
解:连接BC,
由题意可得:OB=OC=BC,
则△OBC是等边三角形,
故sin∠AOC=sin60°=$\frac{\sqrt{3}}{2}$.
故选:D.
点评 此题主要考查了特殊角的三角函数值以及基本作图方法,正确得出△OBC是等边三角形是解题关键.

练习册系列答案
相关题目
9.圆心为P(m,n),半径为1的圆与平面直角坐标系的两坐标轴都相交,则m+n的值可能是( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | 3 |
10.“十年树木,百年树人”,教师的素养关系到国家的未来.扬州市某区招聘音乐教师采用笔试、专业技能测试、说课三种形式进行选拔,这三项的成绩满分均为100分,并按2:3:5的比例折合纳入总分,最后,按照成绩的排序从高到低依次录取.该区要招聘2名音乐教师,通过笔试、专业技能测试筛选出前6名选手进入说课环节,这6名选手的各项成绩见表:
(1)笔试成绩的平均数是76;
(2)写出说课成绩的中位数为85.5,众数为85;
(3)已知序号为1,2,3,4号选手的总分成绩分别为84.2分,84.6分,88.1分,80.8分,请你判断这六位选手中序号是多少的选手将被录用?为什么?
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 笔试成绩 | 66 | 90 | 86 | 64 | 66 | 84 |
| 专业技能测试成绩 | 95 | 92 | 93 | 80 | 88 | 92 |
| 说课成绩 | 85 | 78 | 86 | 88 | 94 | 85 |
(2)写出说课成绩的中位数为85.5,众数为85;
(3)已知序号为1,2,3,4号选手的总分成绩分别为84.2分,84.6分,88.1分,80.8分,请你判断这六位选手中序号是多少的选手将被录用?为什么?
4.菱形的两条对角线长分别为6和8,则菱形的周长是( )
| A. | 40 | B. | 24 | C. | 20 | D. | 10 |
8.以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
| A. | $\frac{\sqrt{3}}{8}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{8}$ |
9.下列运算正确的是( )
| A. | 3x2-x2=3 | B. | a•a3=a3 | C. | a6÷a3=a2 | D. | (a2)3=a6 |
 如图,在Rt△ABC中,∠C=90°,BC=6,AB=10,则tanA=$\frac{3}{4}$.
如图,在Rt△ABC中,∠C=90°,BC=6,AB=10,则tanA=$\frac{3}{4}$. 如图所示,小明在绣湖公园的A处正面观测解百购物中心墙面上的电子屏幕,测得屏幕上端C处的仰角为30°,接着他正对电子屏幕方向前进7m到达B处,又测得该屏幕上端C处的仰角为45°.已知电子屏幕的下端离开地面距离DE为4m,小杨的眼睛离地面1.60m,电子屏幕的上端与墙体的顶端平齐.求电子屏幕上端与下端之间的距离CD(结果保留根号).
如图所示,小明在绣湖公园的A处正面观测解百购物中心墙面上的电子屏幕,测得屏幕上端C处的仰角为30°,接着他正对电子屏幕方向前进7m到达B处,又测得该屏幕上端C处的仰角为45°.已知电子屏幕的下端离开地面距离DE为4m,小杨的眼睛离地面1.60m,电子屏幕的上端与墙体的顶端平齐.求电子屏幕上端与下端之间的距离CD(结果保留根号).