题目内容
7. 如图,在Rt△ABC中,∠C=90°,BC=6,AB=10,则tanA=$\frac{3}{4}$.
如图,在Rt△ABC中,∠C=90°,BC=6,AB=10,则tanA=$\frac{3}{4}$.
分析 根据勾股定理求出AC的长,根据正切的定义解答即可.
解答 解:∵∠C=90°,BC=6,AB=10,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=8,
∴tanA=$\frac{BC}{AC}$=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查的是锐角三角函数的定义和勾股定理的应用,熟记锐角三角函数的定义是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.计算(-3)×4的结果是( )
| A. | 12 | B. | -12 | C. | -1 | D. | -7 |
15. 某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
请根据以上图表信息解答下列问题:
(1)频数分布表中的m=24,n=0.30;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为108;
(3)根据统计数据估计该校1200名中学生中,最喜爱乒乓球这项运动的约有360人.
 某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:| 运动项目 | 频数(人数) | 频率 |
| 篮球 | 30 | 0.25 |
| 羽毛球 | m | 0.20 |
| 乒乓球 | 36 | n |
| 跳绳 | 18 | 0.15 |
| 其它 | 1 | 0.10 |
(1)频数分布表中的m=24,n=0.30;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为108;
(3)根据统计数据估计该校1200名中学生中,最喜爱乒乓球这项运动的约有360人.
2.下列说法正确的是( )
| A. | 抛一枚图钉钉尖着地和钉尖朝上的概率一样大 | |
| B. | 彩票中奖的机会是1%,买100张一定会中奖 | |
| C. | 天气预报说明天下雨的概率是50%,所以明天将有一半的时间在下雨 | |
| D. | 在同一年出生的367名学生中,至少有两人的生日是同一天 |
19.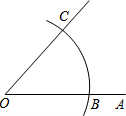 如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为( )
如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为( )
 如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为( )
如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
16.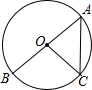 如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则$\widehat{BC}$的长为( )
如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则$\widehat{BC}$的长为( )
 如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则$\widehat{BC}$的长为( )
如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则$\widehat{BC}$的长为( )| A. | $\frac{10}{3}$π | B. | $\frac{10}{9}$π | C. | $\frac{5}{9}$π | D. | $\frac{5}{18}$π |
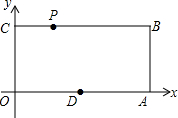 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.
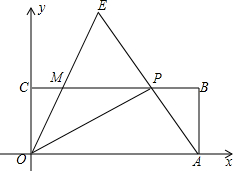 如图,在直角坐标系xOy中,矩形OABC的顶点A、C分别在x轴和y轴正半轴上,点B的坐标是(5,2),点P是CB边上一动点(不与点C、点B重合),连结OP、AP,过点O作射线OE交AP的延长线于点E,交CB边于点M,且∠AOP=∠COM,令CP=x,MP=y.
如图,在直角坐标系xOy中,矩形OABC的顶点A、C分别在x轴和y轴正半轴上,点B的坐标是(5,2),点P是CB边上一动点(不与点C、点B重合),连结OP、AP,过点O作射线OE交AP的延长线于点E,交CB边于点M,且∠AOP=∠COM,令CP=x,MP=y.