题目内容
13.如图甲,在△ABC中,AB=AC,∠BAC=90°.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.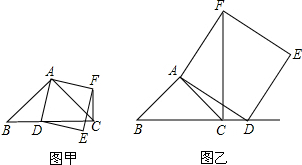
解答下列问题:
(1)当点D在线段BC上时(与点B不重合),如图甲,线段CF、BD之间的位置关系为垂直,数量关系为相等.
(2)当点D在线段BC的延长线上时,如图乙,①中的结论是否仍然成立,为什么?
分析 (1)结论:垂直,相等.只要证明△BAD≌△CAF(SAS),推出CF=BD,推出∠B=∠ACF,推出∠B+∠BCA=90°,推出∠BCA+∠ACF=90°即可;
(2)结论不变.证明方法类似;
解答 解:(1)结论:垂直,相等.
理由∵四边形ADEF是正方形,
∴∠DAF=90°,AD=AF,
∵AB=AC,∠BAC=90°,
∴∠BAD+∠DAC=∠CAF+∠DAC=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$,
∴△BAD≌△CAF(SAS),
∴CF=BD,
∴∠B=∠ACF,
∴∠B+∠BCA=90°,
∴∠BCA+∠ACF=90°,
即CF⊥BD;
故答案为:垂直,相等;
(2)当点D在BC的延长线上时①中的结论仍成立.
理由:∵四边形ADEF是正方形,
∴∠DAF=90°,AD=AF,
∴∠BAC=∠DAF=90°,
∴∠BAD+∠DAC=∠CAF+∠DAC,
即∠BAD=∠CAF,
在△BAD和△CAF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$,
∴△BAD≌△CAF(SAS),
∴CF=BD,
∴∠B=∠ACF,
∵∠B+∠BCA=90°,
∴∠BCA+∠ACF=90°,
即CF⊥BD.
点评 此题考查了正方形的性质、全等三角形的判定与性质以及直角三角形的性质,正确寻找全等三角形的条件是解题的关键是,属于中考常考题型.

练习册系列答案
相关题目
3.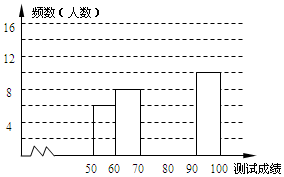 “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
(1)①表中a的值为12; ②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是44%.
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
 “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 6 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 14 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
(1)①表中a的值为12; ②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是44%.
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
1.下列运算错误的是( )
| A. | (x2)3=x6 | B. | x2•x3=x5 | C. | x2-2xy+y2=(x-y)2 | D. | 3x-2x=1 |
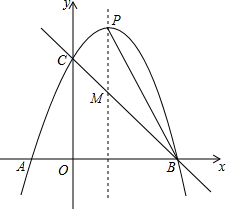 如图,已知抛物线y=-x2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.
如图,已知抛物线y=-x2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB. 如图,将矩形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F.
如图,将矩形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F. 如图,在△ABC中,点D,E分别是AC、AB上的中点,BD与CE相交于点O.求证:OC=2OE.
如图,在△ABC中,点D,E分别是AC、AB上的中点,BD与CE相交于点O.求证:OC=2OE.