题目内容
17. 如图,在△ABC中,点D,E分别是AC、AB上的中点,BD与CE相交于点O.求证:OC=2OE.
如图,在△ABC中,点D,E分别是AC、AB上的中点,BD与CE相交于点O.求证:OC=2OE.
分析 根据三角形中位线定理得出DE∥BC,DE=$\frac{1}{2}$BC,∠OBC=∠ODE,故可得出△ODE∽△OBC,进而可得出结论.
解答 证明:∵点D,E分别是AC、AB上的中点,
∴DE∥BC,DE=$\frac{1}{2}$BC,∠OBC=∠ODE,
∵∠DOE=∠BOC,
∴△ODE∽△OBC,
∴$\frac{OE}{OC}$=$\frac{DE}{BC}$=$\frac{1}{2}$,
∴OC=2OE.
点评 本题考查的是三角形中位线定理,熟知三角形的中位线平行于底边,且等于底边的一半是解答此题的关键.

练习册系列答案
相关题目
14.下列说法中,正确的是( )
| A. | 一组数据-2,-1,0,1,1,2的中位数是0 | |
| B. | 质检部门要了解一批灯泡的使用寿命,应当采用普查的调查方式 | |
| C. | 购买一张福利彩票中奖是一个确定事件 | |
| D. | 分别写有三个数字-1,-2,4的三张卡片(卡片的大小形状都相同),从中任意抽取两张,则卡片上的两数之积为正数的概率为$\frac{1}{3}$ |
5.要从电杆上离地面5m处向地面拉一长为13cm的电缆,则地面电缆固定处与电线杆底部的距离为( )
| A. | 10m | B. | 11m | C. | 12m | D. | 13m |
2.在?ABCD中,对角线AC、BD相交于点O,若BC=12,则AC与BD的值可能是( )
| A. | 8和14 | B. | 10和14 | C. | 10和34 | D. | 18和20 |
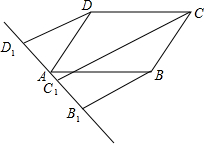 如图,直线l过?ABCD的顶点A,点D1、C1、B1都在直线l上,且DD1∥CC1∥BB1,求证:CC1=DD1+BB1.
如图,直线l过?ABCD的顶点A,点D1、C1、B1都在直线l上,且DD1∥CC1∥BB1,求证:CC1=DD1+BB1. 如图,已知AB∥CD,∠1=140°,则∠2=40°.
如图,已知AB∥CD,∠1=140°,则∠2=40°.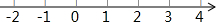 解不等式组$\left\{\begin{array}{l}{5x-2≥3(x-1)}\\{\frac{1}{2}x-1<5-\frac{3}{2}x}\end{array}\right.$,并把解集在所给数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{5x-2≥3(x-1)}\\{\frac{1}{2}x-1<5-\frac{3}{2}x}\end{array}\right.$,并把解集在所给数轴上表示出来.