题目内容
5.先化简,后求值:$\frac{1}{a-1}+\frac{2a-6}{{{a^2}-9}}÷\frac{2a+2}{a+3}$,其中a=tan60°.分析 先将除法转化为乘法,然后计算加法.
解答 解:原式=$\frac{1}{a-1}+\frac{{2({a-3})}}{{({a+3})({a-3})}}×\frac{a+3}{{2({a+1})}}$,
=$\frac{1}{a-1}+\frac{1}{a+1}$,
=$\frac{2a}{{{a^2}-1}}$.
∴当a=tan60°=$\sqrt{3}$时,
原式=$\frac{{2\sqrt{3}}}{{{{({\sqrt{3}})}^2}-1}}=\frac{{2\sqrt{3}}}{2}=\sqrt{3}$.
点评 本题考查了分式的化简求值和特殊角的三角函数值及二次根式的化简,是一道常见题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
14.下列说法中,正确的是( )
| A. | 一组数据-2,-1,0,1,1,2的中位数是0 | |
| B. | 质检部门要了解一批灯泡的使用寿命,应当采用普查的调查方式 | |
| C. | 购买一张福利彩票中奖是一个确定事件 | |
| D. | 分别写有三个数字-1,-2,4的三张卡片(卡片的大小形状都相同),从中任意抽取两张,则卡片上的两数之积为正数的概率为$\frac{1}{3}$ |
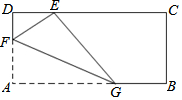 如图,矩形纸片ABCD中,AD=1,将纸片折叠,使顶点A与CD边上的点E重合,折痕FG分别与AD、AB交于点F、G,若DE=$\frac{{\sqrt{3}}}{3}$,则EF的长为$\frac{2}{3}$.
如图,矩形纸片ABCD中,AD=1,将纸片折叠,使顶点A与CD边上的点E重合,折痕FG分别与AD、AB交于点F、G,若DE=$\frac{{\sqrt{3}}}{3}$,则EF的长为$\frac{2}{3}$.
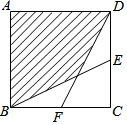 如图,正方形ABCD的边长为2cm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是$\frac{8}{3}$cm2.
如图,正方形ABCD的边长为2cm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是$\frac{8}{3}$cm2. 如图,已知AB∥CD,∠1=140°,则∠2=40°.
如图,已知AB∥CD,∠1=140°,则∠2=40°.