题目内容
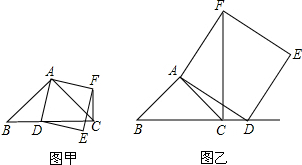
2. 如图,将矩形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F.
如图,将矩形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F.(1)证明:△ADF≌△AB′E;
(2)若AD=12,DC=18,求△AEF的面积.
分析 (1)根据折叠的性质以及矩形的性质,运用ASA即可判定△ADF≌△AB′E;
(2)先设FA=FC=x,则DF=DC-FC=18-x,根据Rt△ADF中,AD2+DF2=AF2,即可得出方程122+(18-x)2=x2,解得x=13. 再根据AE=AF=13,即可得出S△AEF=$\frac{1}{2}•AE•AD$=78.
解答 解: (1)∵四边形ABCD是矩形,
(1)∵四边形ABCD是矩形,
∴∠D=∠C=∠B′=90°,AD=CB=AB′,
∵∠DAF+∠EAF=90°,∠B′AE+∠EAF=90°,
∴∠DAF=∠B′AE,
在△ADF和△AB′E中,
$\left\{\begin{array}{l}{∠D=∠B′}\\{AD=AB′}\\{∠DAF=∠B′AE}\end{array}\right.$,
∴△ADF≌△AB′E(ASA).
(2)由折叠性质得FA=FC,
设FA=FC=x,则DF=DC-FC=18-x,
在Rt△ADF中,AD2+DF2=AF2,
∴122+(18-x)2=x2.
解得x=13.
∵△ADF≌△AB′E(已证),
∴AE=AF=13,
∴S△AEF=$\frac{1}{2}•AE•AD$=$\frac{1}{2}×12×13$=78.
点评 本题属于折叠问题,主要考查了全等三角形的判定与性质,勾股定理以及三角形面积的计算公式的运用,解决问题的关键是:设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
14.下列说法中,正确的是( )
| A. | 一组数据-2,-1,0,1,1,2的中位数是0 | |
| B. | 质检部门要了解一批灯泡的使用寿命,应当采用普查的调查方式 | |
| C. | 购买一张福利彩票中奖是一个确定事件 | |
| D. | 分别写有三个数字-1,-2,4的三张卡片(卡片的大小形状都相同),从中任意抽取两张,则卡片上的两数之积为正数的概率为$\frac{1}{3}$ |
5.要从电杆上离地面5m处向地面拉一长为13cm的电缆,则地面电缆固定处与电线杆底部的距离为( )
| A. | 10m | B. | 11m | C. | 12m | D. | 13m |
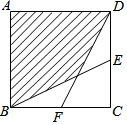 如图,正方形ABCD的边长为2cm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是$\frac{8}{3}$cm2.
如图,正方形ABCD的边长为2cm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是$\frac{8}{3}$cm2.