题目内容
4.一项工程,甲,乙两公司合作,12天可以完成;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.(1)甲,乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,要使乙公司的总施工费较少,则甲公司每天的施工费应低于多少元?
分析 (1)设甲公司单独完成此项工程需x天,则乙工程公司单独完成需1.5x天,根据合作12天完成列出方程求解即可.
(2)设甲每天的施工费y元,则乙每天的施工费(y-1500)元,根据“乙公司的总施工费较少”列出不等式并解答.
解答 解:(1)设甲公司单独做需要x天完成该项工程,则乙公司单独做需要1.5x天完成,
依题意得:$\frac{1}{x}+\frac{1}{1.5x}=\frac{1}{12}$,
去分母,得12×1.5+12=1.5x.
解之,得 x=20.
经检验x=20是原方程的解.
∴1.5x=30
答:甲公司单独做需要20天完成该项工程,则乙公司单独做需要30天完成.
(2)设甲每天的施工费y元,则乙每天的施工费(y-1500)元
由20y>30(y-1500),
解之,得 y<4500.
答:甲每天的施工费应低于4500元.
点评 本题考查了一元一次不等式的应用,分式方程的应用,解题的关键是从实际问题中整理出数量关系并利用该数量关系求解.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
19.中国最大的水果公司“佳沃鑫荣懋”旗下子公司“欢乐果园”购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为P=$\left\{\begin{array}{l}{\frac{1}{4}t+30(1≤t≤24,t为整数)}\\{-\frac{1}{2}t+48(25≤t≤48,t为整数)}\end{array}\right.$,且其日销售量y(kg)与时间t(天)的关系如表:
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售前24天中,子公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
| 时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
| 日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售前24天中,子公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
14.下列说法中,正确的是( )
| A. | 一组数据-2,-1,0,1,1,2的中位数是0 | |
| B. | 质检部门要了解一批灯泡的使用寿命,应当采用普查的调查方式 | |
| C. | 购买一张福利彩票中奖是一个确定事件 | |
| D. | 分别写有三个数字-1,-2,4的三张卡片(卡片的大小形状都相同),从中任意抽取两张,则卡片上的两数之积为正数的概率为$\frac{1}{3}$ |
 在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=$\frac{4}{3}$,点B的坐标为(m,-2).求:
在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=$\frac{4}{3}$,点B的坐标为(m,-2).求: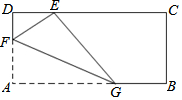 如图,矩形纸片ABCD中,AD=1,将纸片折叠,使顶点A与CD边上的点E重合,折痕FG分别与AD、AB交于点F、G,若DE=$\frac{{\sqrt{3}}}{3}$,则EF的长为$\frac{2}{3}$.
如图,矩形纸片ABCD中,AD=1,将纸片折叠,使顶点A与CD边上的点E重合,折痕FG分别与AD、AB交于点F、G,若DE=$\frac{{\sqrt{3}}}{3}$,则EF的长为$\frac{2}{3}$.