题目内容
2.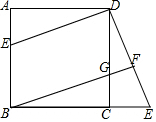 已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=AH,连接BG并延长交DE于F.
已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=AH,连接BG并延长交DE于F.(1)求证:△BCG≌△DCE;
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形,并说明理由.
分析 (1)利用正方形的性质得到BC=CD,∠BCD=90°,则可根据“SAS”证明△BCG≌△DCE;
(2)利用旋转的性质得CE=AE′,则CG=AE′,再根据正方形的性质得BE′∥DG,AB=CD,所以BE′=DG,然后根据平行四边形的判定方法可判断四边形E′BGD是平行四边形.
解答 (1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°,
∴∠BCG=∠DCE,
在△BCG和△DCE中
$\left\{\begin{array}{l}{CB=CD}\\{∠BCG=∠DCE}\\{CG=CE}\end{array}\right.$
∴△BCG≌△DCE;
(2)解:四边形E′BGD是平行四边形.理由如下:
∵△DCE绕D顺时针旋转90°得到△DAE′,
∴CE=AE′,
∵CE=CG,
∴CG=AE′,
∵四边形ABCD是正方形,
∴BE′∥DG,AB=CD,
∴AB-AE′=CD-CG.
即BE′=DG,
∴四边形E′BGD是平行四边形.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质和正方形的性质、平行四边形的判定.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
9.一次函数y=-3x+5图象上有两点A($\frac{2}{3}$,y1)、B(2,y2),则y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | y1≤y2 |
11.已知x-y=-5,xy=3,则x2+y2=( )
| A. | -31 | B. | -25 | C. | 31 | D. | -19 |
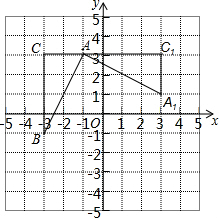 如图,在平面直角坐标系中,有一Rt△ABC,且点A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.
如图,在平面直角坐标系中,有一Rt△ABC,且点A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.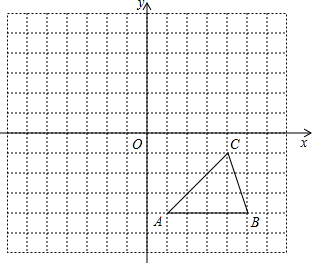 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).