题目内容
19.若m为方程x2-4x+1=0的解,则$\frac{{m}^{2}}{{m}^{4}+{m}^{2}+1}$=$\frac{1}{15}$.分析 根据一元二次方程的解的定义得到m2-4m+1=0,m2=4m-1,m2+1=4m,然后把原式的分子分母进行降次,再约分即可.
解答 解:∵m是方程x2-4x+1=0的解,
∴m2-4m+1=0,
∴m2=4m-1,m2+1=4m
原式=$\frac{{m}^{2}}{{m}^{2}({m}^{2}+1)+1}$=$\frac{{m}^{2}}{(4m-1)4m+1}$=$\frac{{m}^{2}}{16{m}^{2}-4m+1}$=$\frac{4m-1}{16(4m-1)-4m+1}$=$\frac{1}{15}$.
故答案为:$\frac{1}{15}$.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.

练习册系列答案
相关题目
9. 如图,若弧AB半径PA为15,圆心角为120°,半径为2的⊙O,从弧AB的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙O自转的周数是( )
如图,若弧AB半径PA为15,圆心角为120°,半径为2的⊙O,从弧AB的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙O自转的周数是( )
 如图,若弧AB半径PA为15,圆心角为120°,半径为2的⊙O,从弧AB的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙O自转的周数是( )
如图,若弧AB半径PA为15,圆心角为120°,半径为2的⊙O,从弧AB的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙O自转的周数是( )| A. | 5周 | B. | 6周 | C. | 7周 | D. | 8周 |
19.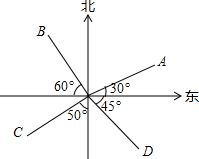 如图,下列说法正确的是( )
如图,下列说法正确的是( )
 如图,下列说法正确的是( )
如图,下列说法正确的是( )| A. | OA的方向是北偏东30° | B. | OB的方向是北偏西60° | ||
| C. | OC的方向是南偏东50° | D. | OD的方向是东偏南45° |
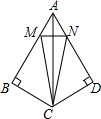 如图,在△ABC中,AB⊥BC,将△ABC沿着AC折叠,得到△ADC,点M、N分别在AB、AD边上,且AM=AN=$\frac{1}{3}$AB,连接MN,若∠BAD=60°,则tan∠MNC的值为3$\sqrt{3}$.
如图,在△ABC中,AB⊥BC,将△ABC沿着AC折叠,得到△ADC,点M、N分别在AB、AD边上,且AM=AN=$\frac{1}{3}$AB,连接MN,若∠BAD=60°,则tan∠MNC的值为3$\sqrt{3}$. 已知,∠DBC和∠BCE分别为△ABC的两个外角,探究∠A和∠DBC,∠BCE之间的数量关系.
已知,∠DBC和∠BCE分别为△ABC的两个外角,探究∠A和∠DBC,∠BCE之间的数量关系.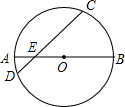 如图,AB是⊙O的直径,E是AB上一点,且AE=3,BE=7,sin∠CEB=$\frac{1}{2}$,求弦CD的长.
如图,AB是⊙O的直径,E是AB上一点,且AE=3,BE=7,sin∠CEB=$\frac{1}{2}$,求弦CD的长.