题目内容
8.一个三位数,百位上的数字等于个位数字与十位上的数字之和,交换百位与十位上的数字位置后,得到的三位数比原来小90,交换十位与个位数字的位置后,得到的三位数比原三位数小9,求原来的三位数.分析 设个位数字为x,十位上的数字为y,则百位上的数字为x+y,根据“交换百位与十位上的数字位置后,得到的三位数比原来小90,”“交换十位与个位数字的位置后,得到的三位数比原三位数小9,”列出方程组解答问题即可.
解答 解:设个位数字为x,十位上的数字为y,由题意得
$\left\{\begin{array}{l}{100(x+y)+10y=100y+10(x+y)+90}\\{10y+x=10x+y+9}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$
则x+y=3
原来的三位数是321.
答:原来的三位数是321.
点评 本题考查了二元一次方程组的应用,掌握数的表示要用数位上的数字乘以数位的计数单位是解决问题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
18.对于反比例函数y=-$\frac{4}{x}$,下列说法正确的是( )
| A. | 经过点(2,2) | B. | y随x的增大而增大 | ||
| C. | 两个分支分布在二、四象限 | D. | 图象关于x轴对称 |
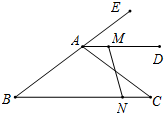 如图,在△ABC中,AB=5cm,BC=8cm,AD为△ABC的外角平分线,且AD∥BC,点M从A出发,以1cm/s的速度沿射线AD匀速运动,同时点N以相同的速度从C出发沿CB匀速向点B运动,当点N到达B时,点M也停止运动.
如图,在△ABC中,AB=5cm,BC=8cm,AD为△ABC的外角平分线,且AD∥BC,点M从A出发,以1cm/s的速度沿射线AD匀速运动,同时点N以相同的速度从C出发沿CB匀速向点B运动,当点N到达B时,点M也停止运动. 如图.在△ABC中,DE∥BC,M为DE上的点,且BM平分∠ABC,CM平分∠ACB.若BD=6,CE=4.则DE=10.
如图.在△ABC中,DE∥BC,M为DE上的点,且BM平分∠ABC,CM平分∠ACB.若BD=6,CE=4.则DE=10.