题目内容
20．
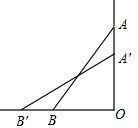如图，一架长2.5m的梯子，斜放在墙上，梯子的底部B离墙角O的距离是0.7m，当梯子的顶部A向下滑0.4m到A′时，梯子的底部向外移动0.8m．
分析 先根据梯子的顶端下滑了0.4米求出A′C的长，再根据勾股定理求出B′C的长，进而可得出结论．
解答 解：∵AB=2.5米，BO=0.7米，
∴AO=$\sqrt{2．{5}^{2}-0．{7}^{2}}$=2.4米，
∵梯子的顶端下滑了0.4米，
∴A′O=2m，
∵在Rt△A′B′C中，A′B′=2.5m，A′C=2m，
∴B′O=$\sqrt{A′B{′}^{2}-A′{O}^{2}}$=$\sqrt{2．{5}^{2}-{2}^{2}}$=1.5m，
∴BB′=B′O-BO=1.5-0.7=0.8m．
故答案为：0.8m．
点评 此题主要考查了勾股定理的应用，关键是掌握勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．
练习册系列答案
相关题目
10．
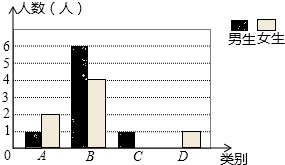某校七年级共有200名学生，在一次数学测验后，为了解本次测验的成绩情况，从中随机抽取了部分学生的成绩进行统计，并制作了如图表：
请你根据以上信息，解答下列问题：
（1）写出a，b，d的值并补全条形图；
（2）请你估计该校七年级共有多少名学生本次成绩不低于80分．
某校七年级共有200名学生，在一次数学测验后，为了解本次测验的成绩情况，从中随机抽取了部分学生的成绩进行统计，并制作了如图表：| 等级 | 分数 | 频数 | 频率 |
| A | 90≤x≤100 | 3 | 0.15 |
| B | 80≤x＜90 | 10 | a |
| C | 70≤x＜80 | b | 0.2 |
| D | 60≤x＜70 | c | d |
| 合计 | 1 |
（1）写出a，b，d的值并补全条形图；
（2）请你估计该校七年级共有多少名学生本次成绩不低于80分．
11．下列解方程的过程，变形正确的是（ ）
| A． | 由$\frac{x}{3}-1=\frac{1-x}{2}$，得2x-1=3-3x | |
| B． | 由$\frac{x-2}{2}-\frac{3x-2}{4}=-1$，得2（x-2）-3x-2=-4 | |
| C． | 由$\frac{y+1}{2}=\frac{y}{3}-\frac{3y-1}{6}$-y，得3y+3=2y-3y+1-6y | |
| D． | 由$\frac{x}{4}$+1=$\frac{0.3x+1}{0.1}$+1.2，得$\frac{x}{4}$+1=$\frac{3x+10}{1}$+12 |
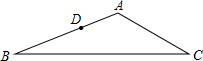如图，在△ABC中，AB=12cm，BC=18cm，AC=9cm，D为AB上一点，BD=$\frac{2}{3}$AB，E是AC上的一点．若△ADE与△ABC相似，请你画出线段DE并求DE的长．
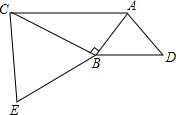如图，△ABC中，∠ABC=90°，以AB、BC分别作等边△ABD和等边△BCE，求证：BD⊥CE．