题目内容
 如图所示,在四边形ABCD中,AD∥BC,AC⊥AB于点A,AD=CD,cosB=
如图所示,在四边形ABCD中,AD∥BC,AC⊥AB于点A,AD=CD,cosB=| 5 |
| 13 |
(1)cos∠DAC的值;
(2)线段AD的长.
考点:解直角三角形
专题:
分析:(1)解直角三角形求出AB,根据勾股定理求出AC,根据平行线性质求出∠DAC=∠ACB,求出cos∠ACB即可;
(2)过D作DE⊥AC于E,根据等腰三角形的性质求出AE=EC=12,根据cos∠DAC=
即可求出答案.
(2)过D作DE⊥AC于E,根据等腰三角形的性质求出AE=EC=12,根据cos∠DAC=
| 12 |
| 13 |
解答:
解:(1)∵AC⊥AB,
∴∠BAC=90°,
∵cosB=
=
,BC=26,
∴AB=10,由勾股定理得:AC=24,
∵AD∥BC,
∴∠DAC=∠ACB,
∴cos∠DAC=cos∠ACB=
=
=
;
(2)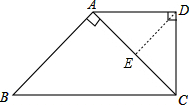
过D作DE⊥AC于E,
∵AD=DC,
∴AE=EC=
×24=12,
∵cos∠DAC=
,
∴
=
,
∴AD=13.
∴∠BAC=90°,
∵cosB=
| AB |
| BC |
| 5 |
| 13 |
∴AB=10,由勾股定理得:AC=24,
∵AD∥BC,
∴∠DAC=∠ACB,
∴cos∠DAC=cos∠ACB=
| AC |
| BC |
| 24 |
| 26 |
| 12 |
| 13 |
(2)

过D作DE⊥AC于E,
∵AD=DC,
∴AE=EC=
| 1 |
| 2 |
∵cos∠DAC=
| 12 |
| 13 |
∴
| AE |
| AD |
| 12 |
| 13 |
∴AD=13.
点评:本题考查了等腰三角形的性质,解直角三角形,勾股定理的应用,能正确解直角三角形是解此题的关键,注意数形结合思想的应用.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
下列各数中是无理数的是( )
| A、-1 | ||
| B、3.141 | ||
C、
| ||
D、
|
 已知等边三角形ABC,D为BC上一点,DE,DF垂直AB,AC,DE=2,DF=1,EF延长线交BC延长线于G,求CG的长?
已知等边三角形ABC,D为BC上一点,DE,DF垂直AB,AC,DE=2,DF=1,EF延长线交BC延长线于G,求CG的长? 如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,AE是⊙O的切线,∠CAE=60°.
如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,AE是⊙O的切线,∠CAE=60°. 如图,点C为线段AB上的一点,AC>BC,已知AB=10,若点C为线段AB的黄金分割点,则BC=
如图,点C为线段AB上的一点,AC>BC,已知AB=10,若点C为线段AB的黄金分割点,则BC= 如图,已知向量
如图,已知向量