题目内容
 如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,AE是⊙O的切线,∠CAE=60°.
如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,AE是⊙O的切线,∠CAE=60°.(1)求∠D的度数;
(2)当BC=4时,求劣弧AC的长.
考点:切线的性质,弧长的计算
专题:
分析:(1)根据切线的性质得出∠BAE=90°,根据∠BAC=∠BAE-∠CAE,求出∠BAC的度数,再根据AB是⊙O的直径,得出∠ABC=90°,求出∠B的度数,再根据∠D=∠B,即可得出∠D的度数;
(2)连接OC,根据OB=OC,∠B=60°,得出△OBC是等边三角形,求出OB=BC=4,∠BOC=60°,从而得出∠AOC=120°,再根据弧长公式即可得出答案.
(2)连接OC,根据OB=OC,∠B=60°,得出△OBC是等边三角形,求出OB=BC=4,∠BOC=60°,从而得出∠AOC=120°,再根据弧长公式即可得出答案.
解答:
解:(1)∵AE是⊙O的切线,
∴AB⊥AE,
∴∠BAE=90°,
∵∠CAE=60°,
∴∠BAC=∠BAE-∠CAE=90°-60°=30°,
∵AB是⊙O的直径,
∴∠ABC=90°,
∴∠B=60°,
∵∠D=∠B,
∴∠D=60°;
(2)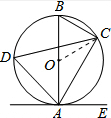 连接OC,
连接OC,
∵OB=OC,∠B=60°,
∴△OBC是等边三角形,
∵BC=4,
∴OB=BC=4,∠BOC=60°,
∴∠AOC=120°,
∴劣弧AC的长是:
=
.
∴AB⊥AE,
∴∠BAE=90°,
∵∠CAE=60°,
∴∠BAC=∠BAE-∠CAE=90°-60°=30°,
∵AB是⊙O的直径,
∴∠ABC=90°,
∴∠B=60°,
∵∠D=∠B,
∴∠D=60°;
(2)
 连接OC,
连接OC,∵OB=OC,∠B=60°,
∴△OBC是等边三角形,
∵BC=4,
∴OB=BC=4,∠BOC=60°,
∴∠AOC=120°,
∴劣弧AC的长是:
| 120π×4 |
| 180 |
| 8π |
| 3 |
点评:此题考查了切线的性质,用到的知识点是圆周角定理、弧长公式、等边三角形的性质等知识.此题难度适中,注意数形结合思想的应用,注意辅助线的作法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,是一个几何体的三视图,则这个几何体的形状是( )
如图,是一个几何体的三视图,则这个几何体的形状是( )| A、圆柱 | B、圆锥 | C、圆台 | D、长方体 |
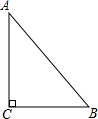 在Rt△ABC中∠C=90°,AB=6,sinA=
在Rt△ABC中∠C=90°,AB=6,sinA=| 2 |
| 3 |
| A、4 | ||||
B、2
| ||||
C、
| ||||
D、
|
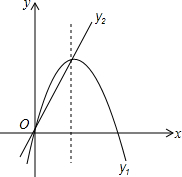 如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较大值记为M;若y1=y2,记M=y1=y2.
如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较大值记为M;若y1=y2,记M=y1=y2. 如图,CB是⊙O的直径,P是CB延长线上一点,PA切⊙O于A点,PA=4cm,PB=2cm,则⊙O的半径为
如图,CB是⊙O的直径,P是CB延长线上一点,PA切⊙O于A点,PA=4cm,PB=2cm,则⊙O的半径为 如图所示,在四边形ABCD中,AD∥BC,AC⊥AB于点A,AD=CD,cosB=
如图所示,在四边形ABCD中,AD∥BC,AC⊥AB于点A,AD=CD,cosB= 如图,∠EOD=70°,射线OC,OB是∠EOA、∠DOA的角平分线.
如图,∠EOD=70°,射线OC,OB是∠EOA、∠DOA的角平分线.