题目内容
 已知等边三角形ABC,D为BC上一点,DE,DF垂直AB,AC,DE=2,DF=1,EF延长线交BC延长线于G,求CG的长?
已知等边三角形ABC,D为BC上一点,DE,DF垂直AB,AC,DE=2,DF=1,EF延长线交BC延长线于G,求CG的长?考点:等边三角形的性质
专题:
分析:先求出BD、CD,再求出CH,根据平行线得出比例式,证出CG=CH.
解答:
解:作EH∥AC,交BC于H;如图所示:
 ∵△ABC是等边三角形,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵DE⊥AB,DF⊥AC,
∴∠BED=∠DFC=90°,
∴BD=
=
=
,CD=
=
=
,
∴CF=
CD=
,
∵EH∥AC,
∴
=
,∠BHE=60°,
∴△BHE是等边三角形,
∴BH=EH=
BD=
,
∴DH=
,
∴CH=DH+CD=
,
∴∴
=
=
,
∴CG=
GH=CH=
.
 ∵△ABC是等边三角形,
∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,
∵DE⊥AB,DF⊥AC,
∴∠BED=∠DFC=90°,
∴BD=
| 2 |
| sin60° |
| 2 | ||||
|
4
| ||
| 3 |
| 1 |
| sin60° |
| 1 | ||||
|
2
| ||
| 3 |
∴CF=
| 1 |
| 2 |
| ||
| 3 |
∵EH∥AC,
∴
| CG |
| GH |
| CF |
| EH |
∴△BHE是等边三角形,
∴BH=EH=
| 1 |
| 2 |
2
| ||
| 3 |
∴DH=
2
| ||
| 3 |
∴CH=DH+CD=
4
| ||
| 3 |
∴∴
| CG |
| GH |
| CF |
| EH |
| 1 |
| 2 |
∴CG=
| 1 |
| 2 |
4
| ||
| 3 |
点评:本题考查了等边三角形的性质、直角三角形的性质以及平行线的性质;通过作辅助平行线得出比例式是解决问题的关键.

练习册系列答案
相关题目
代数式-xy的系数为( )
| A、-2 | B、1 | C、0 | D、-1 |
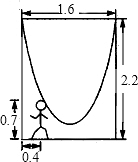 如图,一单杠高2.2米,两立柱之间的距离为1.6米,将一根绳子的两端拴于立柱与铁结合处,绳子自然下垂呈抛物线状态,一身高0.7米的小女孩站在离立柱0.4米处,其头刚好触上绳子,则绳子最低点到地面的距离为( )米.
如图,一单杠高2.2米,两立柱之间的距离为1.6米,将一根绳子的两端拴于立柱与铁结合处,绳子自然下垂呈抛物线状态,一身高0.7米的小女孩站在离立柱0.4米处,其头刚好触上绳子,则绳子最低点到地面的距离为( )米.| A、0.16 | B、0.2 |
| C、0.4 | D、0.64 |
下列四组数中,能组成比例的是( )
| A、1,2,4,5 |
| B、0.2,0.8,12,30 |
| C、12,16,45,60 |
| D、0.1,0.2,0.3,0.4 |
 如图,CB是⊙O的直径,P是CB延长线上一点,PA切⊙O于A点,PA=4cm,PB=2cm,则⊙O的半径为
如图,CB是⊙O的直径,P是CB延长线上一点,PA切⊙O于A点,PA=4cm,PB=2cm,则⊙O的半径为 如图,△ABC三条角平分线相交于O,OE⊥BC,∠BOD=40°,求∠COE.
如图,△ABC三条角平分线相交于O,OE⊥BC,∠BOD=40°,求∠COE. 如图所示,在四边形ABCD中,AD∥BC,AC⊥AB于点A,AD=CD,cosB=
如图所示,在四边形ABCD中,AD∥BC,AC⊥AB于点A,AD=CD,cosB=