题目内容
12.甲乙两人各骑自行车同时从a地出发到b地,并都立即返回,甲的速度较快,当他返回时,在距b地4千米处遇到乙,甲回到a地又立即返回折向B地,在距a地等于全程$\frac{1}{3}$处又遇到从b地返回的乙.求a、b两地间的距离.分析 根据分别用甲、乙的路程除以速度,得出的时间是一样的道理,第一次时间一样的情况下,甲走了(x+4)千米,乙走了(x-4)千米;第二次时间一样的情况下,甲走了2x+$\frac{x}{3}$,乙走了x+$\frac{2x}{3}$.所以依据时间相等列出方程并解答.
解答 解:设a、b两地间的距离x千米,甲乙的速度分别为V1,V2,则
根据两次相遇时间相等得:$\frac{x+4}{{V}_{1}}$=$\frac{x-4}{{V}_{2}}$,①
$\frac{2x+\frac{x}{3}}{{V}_{1}}$=$\frac{x+\frac{2}{3}x}{{V}_{2}}$,②
由②:①并解得x=24.
答:a、b两地间的距离是24千米.
点评 本题考查了分式方程的应用.列分式方程解应用题的一般步骤:设、列、解、验、答.必须严格按照这5步进行做题,规范解题步骤,另外还要注意完整性:如设和答叙述要完整,要写出单位等.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
2.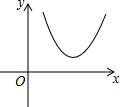 已知二次函数y=ax2+bx+c的图象如图所示,则点(b,c)在( )
已知二次函数y=ax2+bx+c的图象如图所示,则点(b,c)在( )
 已知二次函数y=ax2+bx+c的图象如图所示,则点(b,c)在( )
已知二次函数y=ax2+bx+c的图象如图所示,则点(b,c)在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
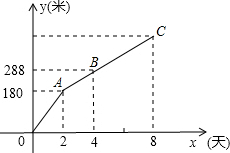 如图,是某工程队在“村村通”工程中修筑的公路长度y(米)与时间x(天)(其中0≤x≤8)之间的关系图象.根据图象提供的信息,求该公路的长.
如图,是某工程队在“村村通”工程中修筑的公路长度y(米)与时间x(天)(其中0≤x≤8)之间的关系图象.根据图象提供的信息,求该公路的长. 如图所示,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动;点Q沿DA边从点D向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动时间(0≤t≤6).那么:
如图所示,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动;点Q沿DA边从点D向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动时间(0≤t≤6).那么: