题目内容
8．约分：（1）-$\frac{6a{b}^{2}}{2b}$；
（2）$\frac{{a}^{2}-{b}^{2}}{{a}^{2}+2ab+{b}^{2}}$．
分析 （1）直接约分即可；
（2）分子利用平方差公式进行因式分解，分母利用完全平方公式进行因式分解，然后约分．
解答 解：（1）原式=-3ab；
（2）原式=$\frac{（a+b）（a-b）}{（a+b）^{2}}$
=$\frac{a-b}{a+b}$．
点评 本题考查了约分．规律方法总结：有约分的概念可知，要首先将分子、分母转化为乘积的形式，再找出分子、分母的最大公因式并约去，注意不要忽视数字系数的约分．
练习册系列答案
相关题目
11．若不等式组$\left\{\begin{array}{l}1＜x≤2\\ x＞k\end{array}\right.$无解，则k的取值范围是（ ）
| A． | k≤2 | B． | k＜1 | C． | k≥2 | D． | 1≤k＜2 |
3．下列各式的约分，正确的是（ ）
| A． | $\frac{-a-b}{a-b}$=1 | B． | $\frac{-a-b}{a-b}$=-1 | C． | $\frac{{a}^{2}-{b}^{2}}{a+b}$=a-b | D． | $\frac{{a}^{2}-{b}^{2}}{a+b}$=a+b |
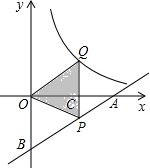如图，一次函数y=$\frac{1}{2}$x-2的图象分别交x轴、y轴于A、B，P为AB上一点且PC为△AOB的中位线，PC的延长线交反比例函数y=$\frac{5}{x}$（x＞0）的图象于Q，则S△OQP=$\frac{7}{2}$．
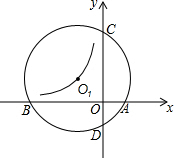如图，⊙O1与坐标轴交于A、B、C、D四点，A（2，0）、B（-6，0）、D（0，-2），反比例函数y=$\frac{k}{x}$过O1，则k=-4．