题目内容
3．
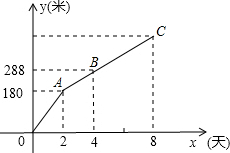如图，是某工程队在“村村通”工程中修筑的公路长度y（米）与时间x（天）（其中0≤x≤8）之间的关系图象．根据图象提供的信息，求该公路的长．
分析 本题可设x≥2时，函数解析式为y=kx+b，根据待定系数法即可求出函数解析式，进而即可求出答案．
解答 解：设x≥2时，函数解析式为y=kx+b，
∴2k+b=180，4k+b=288，
解得k=54，b=72，
∴y=54x+72，
∴当x=8时，y=504．
答：该公路长504米．
点评 本题考查一次函数的应用，关键是根据两点，可确定直线的函数解析式．当已知函数的某一点的横坐标时，也可求出相应的y值．
练习册系列答案
相关题目
11．若不等式组$\left\{\begin{array}{l}1＜x≤2\\ x＞k\end{array}\right.$无解，则k的取值范围是（ ）
| A． | k≤2 | B． | k＜1 | C． | k≥2 | D． | 1≤k＜2 |
18．
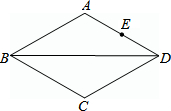如图，在菱形ABCD中，AB=4，∠ABC=60°，E为AD中点，P为对角线BD上一动点，连结PA和PE，则PA+PE的值最小是（ ）
如图，在菱形ABCD中，AB=4，∠ABC=60°，E为AD中点，P为对角线BD上一动点，连结PA和PE，则PA+PE的值最小是（ ）| A． | 2 | B． | 4 | C． | $\sqrt{3}$ | D． | $2\sqrt{3}$ |
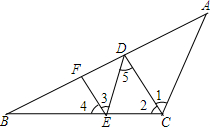已知：如图，AC∥DE，DC∥EF，CD平分∠BCD．求证：EF平分∠BED．