题目内容
7．设M=a2（b2+1），N=2ab-4a-5，其中a，b为实数，若M=N，则式子ba的值是4．分析 根据题意得到a2（b2+1）=2ab-4a-5，将该等式利用配方法转化为（ab-1）2+（a+2）2=0，利用非负数的性质求得a、b的值，将其代入所求的代数式进行求值即可．
解答 解：依题意得：a2（b2+1）=2ab-4a-5，
整理，得
（ab-1）2+（a+2）2=0，
所以ab=1，a=-2．
则b=-$\frac{1}{2}$，
所以ba=（-$\frac{1}{2}$）-2=4．
故答案是：4．
点评 本题考查了非负数的性质和配方法的应用．解题时要注意配方法的步骤．注意在变形的过程中不要改变式子的值．
练习册系列答案
相关题目
18．
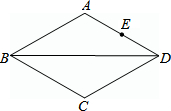如图，在菱形ABCD中，AB=4，∠ABC=60°，E为AD中点，P为对角线BD上一动点，连结PA和PE，则PA+PE的值最小是（ ）
如图，在菱形ABCD中，AB=4，∠ABC=60°，E为AD中点，P为对角线BD上一动点，连结PA和PE，则PA+PE的值最小是（ ）| A． | 2 | B． | 4 | C． | $\sqrt{3}$ | D． | $2\sqrt{3}$ |
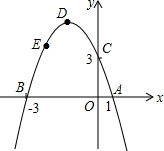若抛物线的顶点为点D（-1，4），点E（-2，n）在抛物线上，x轴，y轴上是否存在点P，Q，使四边形PQDE的周长最小？若存在，求出最小值；若不存在，请说明理由．
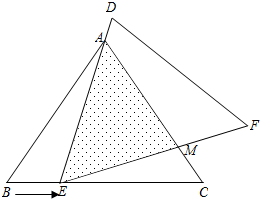如图，在△ABC中，己知AB=AC=5，BC=6，且将△ABC≌△DEF，将△DEF与△ABC重合在一起，△ABC不动，△DEF运动，并满足：点E在边BC上沿B到C的方向运动，且DE始终经过点A，EF与AC交于M点．
3．下列各式的约分，正确的是（ ）
| A． | $\frac{-a-b}{a-b}$=1 | B． | $\frac{-a-b}{a-b}$=-1 | C． | $\frac{{a}^{2}-{b}^{2}}{a+b}$=a-b | D． | $\frac{{a}^{2}-{b}^{2}}{a+b}$=a+b |